Difference between revisions of "GHC/Data Parallel Haskell"
| Line 161: | Line 161: | ||
We compile and link the program as described above. |
We compile and link the program as described above. |
||
| − | '''NOTE:''' The code as presented is unsuitable for benchmarking as we wouldn't want to measure the purely sequential random number generation (that dominates this simple program). For benchmarking, we would want to guarantee that the generated vectors are fully evaluated before taking the time. The module [http://www.haskell.org/ghc/docs/latest/html/libraries/dph-par/Data-Array-Parallel-PArray.html Data.Array.Parallel.PArray] exports the function <hask>nf</hask> for this purpose. |
+ | '''NOTE:''' The code as presented is unsuitable for benchmarking as we wouldn't want to measure the purely sequential random number generation (that dominates this simple program). For benchmarking, we would want to guarantee that the generated vectors are fully evaluated before taking the time. The module [http://www.haskell.org/ghc/docs/latest/html/libraries/dph-par/Data-Array-Parallel-PArray.html Data.Array.Parallel.PArray] exports the function <hask>nf</hask> for this purpose. A variant of the dot-product example code that determines the CPU time consumed by <hask>dotp_wrapper</hask> is at [wiki:GHC/Data Parallel Haskell/MainTimed]. |
==== Parallel execution ==== |
==== Parallel execution ==== |
||
Revision as of 04:30, 25 January 2011
Data Parallel Haskell
Data Parallel Haskell is the codename for an extension to the Glasgow Haskell Compiler and its libraries to support nested data parallelism with a focus to utilise multicore CPUs. Nested data parallelism extends the programming model of flat data parallelism, as known from parallel Fortran dialects, to irregular parallel computations (such as divide-and-conquer algorithms) and irregular data structures (such as sparse matrices and tree structures). An introduction to nested data parallelism in Haskell, including some examples, can be found in the paper Nepal – Nested Data-Parallelism in Haskell.
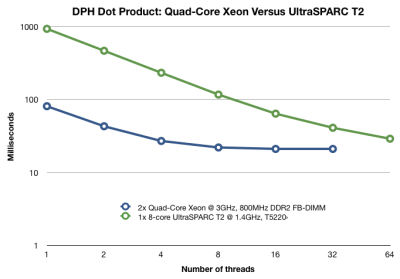
This is the performance of a dot product of two vectors of 10 million doubles each using Data Parallel Haskell. Both machines have 8 cores. Each core of the T2 has 8 hardware thread contexts.
Project status
We are currently preparing for a release of Data Parallel Haskell (DPH) for GHC 7.2. All major components of DPH are implemented, including code vectorisation and parallel execution on multicore systems. However, the implementation has many limitations and probably also many bugs. Major limitations include the inability to mix vectorised and non-vectorised code in a single Haskell module, the need to use a feature-deprived, special-purpose Prelude in vectorised code, and a lack of optimisations (leading to poor performance in some cases).
The current implementation should work well for code with nested parallelism, where the depth of nesting is statically fixed. It should also perform reasonably when nesting is recursive as long as no user-defined nested-parallel datatypes are used. Support for user-defined nested-parallel datatypes is still rather experimental and will likely result in inefficient code. For concrete examples of the various classes of parallelism, please refer to the DPH benchmark status page.
DPH focuses on irregular data parallelism. For regular data parallel code in Haskell, please consider using the companion library Repa, which builds on the parallel array infrastructure of DPH.
Disclaimer: Data Parallel Haskell is very much work in progress. Some components are already usable, and we explain here how to use them. However, please be aware that APIs are still in flux and functionality may change during development.
Where to get it
To get DPH, you currently need to get the development version of GHC, which automatically includes DPH. We are in the process of preparing a DPH release for GHC 7.0, the current stable release of GHC.
Overview
From a user's point of view, Data Parallel Haskell adds a new data type to Haskell –namely, parallel arrays– as well as operations on parallel arrays. Syntactically, parallel arrays are like lists, only that instead of square brackets [ and ], parallel arrays use square brackets with a colon [: and :]. In particular, [:e:] is the type of parallel arrays with elements of type e; the expression [:x, y, z:] denotes a three element parallel array with elements x, y, and z; and [:x + 1 | x <- xs:] represents a simple array comprehension. More sophisticated array comprehensions (including the equivalent of parallel list comprehensions) as well as enumerations and pattern matching proceed in an analog manner. Moreover, the array library of DPH defines variants of most list operations from the Haskell Prelude and the standard List library (e.g., we have lengthP, sumP, mapP, and so on).
The two main differences between lists and parallel arrays are that (1) parallel arrays are a strict data structure and (2) that they are not inductively defined. Parallel arrays are strict in that by demanding a single element, all elements of an array are demanded. Hence, all elements of a parallel array might be evaluated in parallel. To facilitate such parallel evaluation, operations on parallel arrays should treat arrays as aggregate structures that are manipulated in their entirety (instead of the inductive, element-wise processing that is the foundation of all Haskell list functions.)
As a consequence, parallel arrays are always finite, and standard functions that yield infinite lists, such as enumFrom and repeat, have no corresponding array operation. Moreover, parallel arrays only have an undirected fold function foldP that requires an associative function as an argument – such a fold function has a parallel step complexity of O(log n) for arrays of length n. Parallel arrays also come with some aggregate operations that are absent from the standard list library, such as permuteP.
A simple example
As a simple example of a DPH program, consider the following code that computes the dot product of two vectors given as parallel arrays:
dotp :: Num a => [:a:] -> [:a:] -> a
dotp xs ys = sumP [:x * y | x <- xs | y <- ys:]
This code uses an array variant of parallel list comprehensions, which could alternatively be written as [:x * y | (x, y) <- zipP xs ys:], but should otherwise be self-explanatory to any Haskell programmer.
Running DPH programs
Unfortunately, we cannot use the above implementation of dotp directly in the current preliminary implementation of DPH. In the following, we will discuss how the code needs to be modified and how it needs to be compiled and run for parallel execution. GHC applies an elaborate transformation to DPH code, called vectorisation, that turns nested into flat data parallelism. This transformation is only useful for code that is executed in parallel (i.e., code that manipulates parallel arrays), but for parallel code it dramatically simplifies load balancing.
No type classes
Unfortunately, vectorisation does not handle type classes at the moment. Hence, we currently need to avoid overloaded operations in parallel code. To account for that limitation, we specialise dotp on doubles.
dotp_double :: [:Double:] -> [:Double:] -> Double
dotp_double xs ys = sumP [:x * y | x <- xs | y <- ys:]
Special Prelude
As the current implementation of vectorisation cannot handle some language constructs, we cannot use it to vectorise those parts of the standard Prelude that might be used in parallel code (such as arithmetic operations). Instead, DPH comes with its own (rather limited) Prelude in Data.Array.Parallel.Prelude plus three extra modules to support one numeric type each Data.Array.Parallel.Prelude.Float, Data.Array.Parallel.Prelude.Double, Data.Array.Parallel.Prelude.Int, and Data.Array.Parallel.Prelude.Word8. These four modules support the same functions (on different types) and if a program needs to use more than one, they need to be imported qualified (as we cannot use type classes in vectorised code in the current version). Moreover, we have Data.Array.Parallel.Prelude.Bool. If your code needs any other numeric types or functions that are not implemented in these Prelude modules, you currently need to implement and vectorise that functionality yourself.
To compile dotp_double, we add the following three import statements:
import qualified Prelude
import Data.Array.Parallel.Prelude
import Data.Array.Parallel.Prelude.Double
Impedance matching
Special care is needed at the interface between vectorised and non-vectorised code. Currently, only simple types can be passed between these different kinds of code. In particular, parallel arrays (which might be nested) cannot be passed. Instead, we need to pass flat arrays of type PArray. This type is exported by our special-purpose Prelude together with a conversion function fromPArrayP (which is specific to the element type due to the lack of type classes in vectorised code).
Using this conversion function, we define a wrapper function for dotp_double that we export and use from non-vectorised code.
dotp_wrapper :: PArray Double -> PArray Double -> Double
{-# NOINLINE dotp_wrapper #-}
dotp_wrapper v w = dotp_double (fromPArrayP v) (fromPArrayP w)
It is important to mark this function as NOINLINE as we don't want it to be inlined into non-vectorised code.
Compiling vectorised code
The syntax for parallel arrays is an extension to Haskell 2010 that needs to be enabled with the language option ParallelArrays. Furthermore, we need to explicitly tell GHC if we want to vectorise a module by using the -fvectorise option.
Currently, GHC either vectorises all code in a module or none. This can be inconvenient as some parts of a program cannot be vectorised – for example, code in the IO monad (the radical re-ordering of computations performed by the vectorisation transformation is only valid for pure code). As a consequence, the programmer currently needs to partition vectorised and non-vectorised code carefully over different modules.
Overall, we get the following complete module definition for the dot-product code:
{-# LANGUAGE ParallelArrays #-}
{-# GHC_OPTIONS -fvectorise #-}
module DotP (dotp_wrapper)
where
import qualified Prelude
import Data.Array.Parallel.Prelude
import Data.Array.Parallel.Prelude.Double
dotp_double :: [:Double:] -> [:Double:] -> Double
dotp_double xs ys = sumP [:x * y | x <- xs | y <- ys:]
dotp_wrapper :: PArray Double -> PArray Double -> Double
{-# NOINLINE dotp_wrapper #-}
dotp_wrapper v w = dotp_double (fromPArrayP v) (fromPArrayP w)
Assuming the module is in a file DotP.hs, we compile it as follows:
ghc -c -Odph -fdph-par DotP.hs
The option -Odph enables a predefined set of GHC optimisation options that works best for DPH code and -fdph-par selects the standard parallel DPH backend library. (This is currently the only relevant backend, but there may be others in the future.)
Using vectorised code
Finally, we need a main module that calls the vectorised code, but is itself not vectorised, so that it may contain I/O. In this simple example, we convert two simple lists to parallel arrays, compute their dot product, and print the result:
import Data.Array.Parallel.PArray (PArray, fromList)
import DotP (dotp_wrapper) -- import vectorised code
main :: IO ()
main
= let v = fromList [1..10] -- convert lists...
w = fromList [1,2..20] -- ...to parallel arrays
result = dotp_wrapper v w -- invoke vectorised code
in
print result -- print the result
We compile this module with
ghc -c -Odph -fdph-par Main.hs
and finally link the two modules into an executable dotp with
ghc -o dotp -threaded -fdph-par DotP.o Main.o
We need the -threaded option to link with GHC's multi-threaded runtime and -fdph-par to link with the standard parallel DPH backend.
Generating input data
To see any benefit from parallel execution, a data-parallel program needs to operate on a sufficiently large data set. Hence, instead of two small constant vectors, we might want to generate some larger input data:
import System.Random (newStdGen)
import Data.Array.Parallel.PArray (PArray, randomRs)
import DotP (dotp_wrapper) -- import vectorised code
main :: IO ()
main
= do
gen1 <- newStdGen
gen2 <- newStdGen
let v = randomRs n range gen1
w = randomRs n range gen2
print $ dotp_wrapper v w -- invoke vectorised code and print the result
where
n = 10000 -- vector length
range = (-100, 100) -- range of vector elements
We compile and link the program as described above.
NOTE: The code as presented is unsuitable for benchmarking as we wouldn't want to measure the purely sequential random number generation (that dominates this simple program). For benchmarking, we would want to guarantee that the generated vectors are fully evaluated before taking the time. The module Data.Array.Parallel.PArray exports the function nf for this purpose. A variant of the dot-product example code that determines the CPU time consumed by dotp_wrapper is at [wiki:GHC/Data Parallel Haskell/MainTimed].
Parallel execution
The array library of DPH comes in two flavours: dph-seq and dph-par. The former supports the whole DPH stack, but only executes on a single core. In contrast, dph-par implements multi-threaded code.
In the above compiler invocations, we used the option -fdph-seq to select the dph-seq flavour. We can as well compile with -fdph-par to generate multi-threaded code. By invoking ./dotp +RTS -N2, we use two OS threads to execute the program. A beautiful property of DPH is that the number of threads used to execute a program only affects its performance, but not the result. So, it is fine to do all debugging concerning correctness with dph-seq and to switch to dph-par only for performance debugging.
Data Parallel Haskell –and more generally, GHC's multi-threading support– currently only aims at multicore processors or uniform memory access (UMA) multi-processors. Performance on non-uniform memory access (NUMA) machines is generally bad as GHC's runtime makes no effort at optimising placement. Some people have reported that the parallel garbage collector (as included in GHC 6.10.1) should not be used with parallel programs; i.e., it is advisable to start parallel programs with my_program +RTS -N2 -g1 to run on two cores (and different arguments to -N for other core counts). This problem has been addressed in the development version of GHC.
Further examples
Further examples are available in the examples directory of the package dph source. In addition to code using vectorisation (as described above), these examples also contain code that directly targets the two array libraries contained in -package dph-seq and -package dph-par, respectively. For more complex programs, targeting the DPH array libraries directly can lead to much faster code than using vectorisation, as GHC currently doesn't optimise vectorised code very well. However, code targeting the DPH libraries directly can only use flat data parallelism.
The interfaces of the various components of the DPH library are specified in GHC's hierarchical libraries documentation.
Designing parallel programs
Data Parallel Haskell is a high-level language to code parallel algorithms. Like plain Haskell, DPH frees the programmer from many low-level operational considerations (such as thread creation, thread synchronisation, critical sections, and deadlock avoidance). Nevertheless, the full responsibility for parallel algorithm design and many performance considerations (such as when does a computation have sufficient parallelism to make it worthwhile to exploit that parallelism) are still with the programmer.
DPH encourages a data-driven style of parallel programming and, in good Haskell tradition, puts the choice of data types first. Specifically, the choice between using lists or parallel arrays for a data structure determines whether operations on the structure will be executed sequentially or in parallel. In addition to suitably combining standard lists and parallel arrays, it is often also useful to embed parallel arrays in a user-defined inductive structure, such as the following definition of parallel rose trees:
data RTree a = RNode [:RTree a:]
The tree is inductively defined; hence, tree traversals will proceed sequentially, level by level. However, the children of each node are held in parallel arrays, and hence, may be traversed in parallel. This structure is, for example, useful in parallel adaptive algorithms based on a hierarchical decomposition, such as the Barnes-Hut algorithm for solving the N-body problem as discussed in more detail in the paper Harnessing the Multicores: Nested Data Parallelism in Haskell.
For a general introduction to nested data parallelism and its cost model, see Blelloch's Programming Parallel Algorithms.
Further reading and information on the implementation
DPH has two major components: (1) the vectorisation transformation and (2) the generic DPH library for flat parallel arrays. The vectorisation transformation turns nested into flat data-parallelism and is described in detail in the paper Harnessing the Multicores: Nested Data Parallelism in Haskell. The generic array library maps flat data-parallelism to GHC's multi-threaded multicore support and is described in the paper Data Parallel Haskell: a status report. The same topics are also covered in the slides for the two talks Nested data parallelism in Haskell and Compiling nested data parallelism by program transformation.
For further reading, consult this collection of background papers, and pointers to other people's work. If you are really curious and like to know implementation details and the internals of the Data Parallel Haskell project, much of it is described on the GHC developer wiki on the pages covering data parallelism and type families.
Feedback
Please file bug reports at GHC's bug tracker. Moreover, comments and suggestions are very welcome. Please post them to the GHC user's mailing list, or contact the DPH developers directly: