Difference between revisions of "LGtk/ADT lenses"
(begin to document ADT lenses) |
(add figure and link) |
||
| Line 90: | Line 90: | ||
* With <hask>tailLens = sndLens . sndLens :: Lens S Int</hask> the tail of the list can be viewed and edited. |
* With <hask>tailLens = sndLens . sndLens :: Lens S Int</hask> the tail of the list can be viewed and edited. |
||
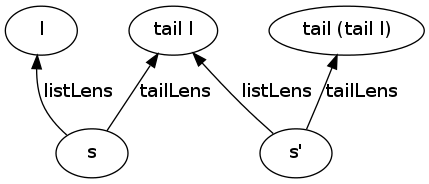
| − | Note that for editing the tail of the list, we need <hask>s' :: S</hask> such that <hask>s</hask> viewed through <hask>tailLens</hask> is the same as <hask>s'</hask> viewed through <hask>listLens</hask>. Explained on a figure: |
+ | Note that for editing the tail of the list, we need an <hask>s' :: S</hask> such that <hask>s</hask> viewed through <hask>tailLens</hask> is the same as <hask>s'</hask> viewed through <hask>listLens</hask>. Explained on a figure: |
| − | |||
| + | [[Image:ADT.png]] |
||
| + | How <hask>s'</hask> is a related, but different question. See [[LGtk/Semantics#Dependent_reference_creation]]. |
||
== Links and references == |
== Links and references == |
||
Revision as of 18:26, 7 June 2013
Problem description
Lenses provide uniform and compositional way to view and edit data structures.
For example, one can view and edit pairs with fstLens and sndLens. fstLens and sndLens forms a complete toolbox for editing pairs in the sense that given pairs p :: (a, b) and q :: (a, b), with succesive get and set operations p can be changed to be equivalent to q: setL fstLens (getL fstLens q) $ setL sndLens (getL sndLens q) p.
Similarly, there is a complete toolbox of lenses for records, the toolbox contains one lens for each record field.
Now, the problem is, are there a toolbox of lenses for algebraic data types with multiple constructors?
Existing solutions
Partial lenses
The data-lens library provides partial lenses which are isomorphic to
type PartialLens a b = (a -> Maybe b, a -> Maybe (b -> a))
The flollowing partial lenses are defined for lists:
headLens :: PartialLens [a] a
headLens = (get, set)
where
get [] = Nothing
get (h:t) = Just h
set [] = Nothing
set (h:t) = Just (:t)
tailLens :: PartialLens [a] [a]
tailLens = (get, set)
where
get [] = Nothing
get (h:t) = Just t
set [] = Nothing
set (h:t) = Just (h:)
Unfortunately headLens and tailLens does not provide a complete toolbox, one cannot change an empty list to a non-empty list with them, for example.
Other solutions
Please help to extend the list of known solutions.
ADT lenses
The proposed solution, summarized:
Use one lens for each ADT type, with reversed direction.
Example: List lens
The ADT lens for lists:
import Data.Lens.Common
listLens :: Lens (Bool, (a, [a])) [a]
listLens = lens get set where
get (False, _) = []
get (True, (l, r)) = l: r
set [] (_, x) = (False, x)
set (l: r) _ = (True, (l, r))
Usage
Suppose that we have a state s of type
type S = (Bool, (Int, [Int]))
If we view the state through listLens :: Lens S [Int], we see a list of Ints. So we can view the list.
We can edit the list with the following lenses:
- With
fstLens :: Lens S Boolthe top level constructor of the list can be viewed and edited:Falsecorresponds to[]andTruecorresponds to(:). - With
headLens = fstLens . sndLens :: Lens S Intthe first element of the list can be viewed and edited. Note that if the top level constructor of the list is[], the first element can still be edited; the change will only be visible throughlistLenswhen the constructor is changed back to(:). (This may seem to be odd, but for certain applications this is the right behaviour.) - With
tailLens = sndLens . sndLens :: Lens S Intthe tail of the list can be viewed and edited.
Note that for editing the tail of the list, we need an s' :: S such that s viewed through tailLens is the same as s' viewed through listLens. Explained on a figure:
How s' is a related, but different question. See LGtk/Semantics#Dependent_reference_creation.
Links and references
I have not seen this technique described before. Please help to extend the list of papers / blog entries, where this or similar technique is used.
[Reddit comments]