Difference between revisions of "Numeric Haskell: A Repa Tutorial"
(→Example: matrix-matrix multiplication: - update to Repa 3.2) |
|||
| Line 732: | Line 732: | ||
== Example: matrix-matrix multiplication == |
== Example: matrix-matrix multiplication == |
||
| − | A more advanced example from the Repa paper |
+ | A more advanced example from the Repa paper is matrix-matrix multiplication. The result of matrix multiplication is a matrix whose elements are found by multiplying the elements of each row from the first matrix by the associated elements of the same column from the second matrix and summing the result. |
| − | matrix multiplication is a matrix whose elements are found by |
||
| − | multiplying the elements of each row from the first matrix by the |
||
| − | associated elements of the same column from the second matrix and |
||
| − | summing the result. |
||
if <math>A=\begin{bmatrix}a&b\\c&d\end{bmatrix}</math> and <math>B=\begin{bmatrix}e&f\\g&h\end{bmatrix}</math> |
if <math>A=\begin{bmatrix}a&b\\c&d\end{bmatrix}</math> and <math>B=\begin{bmatrix}e&f\\g&h\end{bmatrix}</math> |
||
| Line 748: | Line 744: | ||
<haskell> |
<haskell> |
||
| − | + | mmMult :: Monad m |
|
| − | + | => Array U DIM2 Double |
|
| − | + | -> Array U DIM2 Double |
|
| − | + | -> m (Array U DIM2 Double) |
|
| ⚫ | |||
| − | |||
| ⚫ | |||
| ⚫ | |||
| + | t = transpose2D b |
||
| ⚫ | |||
| − | + | aRepl = extend (Z :.All :.colsB :.All) a |
|
| − | + | bRepl = extend (Z :.rowsA :.All :.All) t |
|
| − | + | (Z :.colsA :.rowsA) = extent a |
|
| − | + | (Z :.colsB :.rowsB) = extent b |
|
| − | (Z :.colsB :.rowsB) = extent b |
||
</haskell> |
</haskell> |
||
The idea is to expand both 2D argument arrays into 3D arrays by |
The idea is to expand both 2D argument arrays into 3D arrays by |
||
| − | replicating them across a new axis. The front face of the cuboid that |
+ | replicating them across a new axis using <code>extend</code> function. The front face of the cuboid that results represents the array <code>a</code>, which we replicate as often as <code>b</code> has columns <code>(colsB)</code>, producing <code>aRepl</code>. |
| − | results represents the array <code>a</code>, which we replicate as often |
||
| − | as <code>b</code> has columns <code>(colsB)</code>, producing |
||
| − | <code>aRepl</code>. |
||
The top face represents <code>t</code> (the transposed b), which we |
The top face represents <code>t</code> (the transposed b), which we |
||
replicate as often as a has rows <code>(rowsA)</code>, producing |
replicate as often as a has rows <code>(rowsA)</code>, producing |
||
<code>bRepl,</code>. The two replicated arrays have the same extent, |
<code>bRepl,</code>. The two replicated arrays have the same extent, |
||
| − | which corresponds to the index space of matrix multiplication |
+ | which corresponds to the index space of matrix multiplication. |
Optimized implementations of this function are available in the |
Optimized implementations of this function are available in the |
||
Revision as of 08:42, 11 October 2012
Note: This tutorial is for an old version of Repa. The current version (Repa 3.1) has a slightly different API. You can read more about Repa 3 in this paper.
Repa is a Haskell library for high performance, regular, multi-dimensional parallel arrays. All numeric data is stored unboxed and functions written with the Repa combinators are automatically parallel (provided you supply "+RTS -N" on the command line when running the program).
This document provides a tutorial on array programming in Haskell using the repa package.
Note: a companion tutorial to this is provided as the vector tutorial, and is based on the NumPy tutorial.
Authors: Don Stewart.
Quick Tour
Repa (REgular PArallel arrays) is an advanced, multi-dimensional parallel arrays library for Haskell, with a number of distinct capabilities:
- The arrays are "regular" (i.e. dense, rectangular and store elements all of the same type); and
- Functions may be written that are polymorphic in the shape of the array;
- Many operations on arrays are accomplished by changing only the shape of the array (without copying elements);
- The library will automatically parallelize operations over arrays.
This is a quick start guide for the package. For further information, consult:
- The Haddock Documentation
- Regular, Shape-polymorphic, Parallel Arrays in Haskell.
- Efficient Parallel Stencil Convolution in Haskell
Importing the library
Download the `repa` package:
$ cabal install repa
and import it qualified:
import qualified Data.Array.Repa as R
The library needs to be imported qualified as it shares the same function names as list operations in the Prelude.
Note: Operations that involve writing new index types for Repa arrays will require the '-XTypeOperators' language extension.
For non-core functionality, a number of related packages are available:
- repa-io
- repa-algorithms
- repa-devil (image loading)
and example algorithms in:
Type indexes
Repa 3 introduced a notion of type index:
data family Array rep sh e
In the above definition rep is the type index, which is represented with a data type name and defines the type of underlying array representation. This allows to explicitly specify representation of an array on type system level. Repa distinguishes ten different types of representation, which fall into three categories: manifest, delayed and meta. Manifest arrays are represented by concrete values stored in memory using e.g. unboxed vectors (represented with data type U) or strict bytestrings (B). Delayed array (D) is a function from index to a value. Every time an element is requested from a delayed array it is calculated anew, which means that delayed arrays are inefficient when the data is needed multiple times. On the other hand delaying an array allows to perform optimisation by fusion. Meta arrays provide additional information about underlying array data, which can be used for load balancing or speeding up calculation of border effects. See Guiding Parallel Array Fusion with Indexed Types paper for a detailed explanation of each representation.
Array shapes
Before we can get started manipulating arrays, we need a grasp of repa's notion of array shape. Much like the classic 'array' library in Haskell, repa-based arrays are parameterized via a type which determines the dimension of the array, and the type of its index. However, while classic arrays take tuples to represent multiple dimensions, Repa arrays use a richer type language for describing multi-dimensional array indices and shapes (technically, a heterogeneous snoc list).
Shape types are built somewhat like lists. The constructor Z corresponds
to a rank zero shape, and is used to mark the end of the list. The :. constructor adds additional dimensions to the shape. So, for example, the shape:
(Z :. 3 :. 2 :. 3)
is the shape of a small 3D array, with shape type
(Z :. Int :. Int :. Int)
The most common dimensions are given by the shorthand names:
type DIM0 = Z
type DIM1 = DIM0 :. Int
type DIM2 = DIM1 :. Int
type DIM3 = DIM2 :. Int
type DIM4 = DIM3 :. Int
type DIM5 = DIM4 :. Int
thus,
Array U DIM2 Double
is the type of a two-dimensional array of unboxed doubles, indexed via Int keys, while
Array U Z Double
is a zero-dimension object (i.e. a point) holding an unboxed Double.
Many operations over arrays are polymorphic in the shape / dimension
component. Others require operating on the shape itself, rather than
the array. A typeclass, Shape, lets us operate uniformly
over arrays with different shape.
Building shapes
To build values of shape type, we can use the Z and :. constructors. Open the ghci and import Repa:
ghci> :m +Data.Array.Repa
ghci> Z -- the zero-dimension
Z
For arrays of non-zero dimension, we must give a size. Note: a common error is to leave off the type of the size.
ghci> :t Z :. 10
Z :. 10 :: Num head => Z :. head
leading to annoying type errors about unresolved instances, such as:
No instance for (Shape (Z :. head0))
To select the correct instance, you will need to annotate the size literals with their concrete type:
ghci> :t Z :. (10 :: Int)
Z :. (10 :: Int) :: Z :. Int
is the shape of 1D arrays of length 10, indexed via Ints.
Given an array, you can always find its shape by calling extent.
Additional convenience types for selecting particular parts of a shape are also provided (All, Any, Slice etc.) which are covered later in the tutorial.
Working with shapes
That one key operation, extent, gives us many attributes of an array:
-- Extract the shape of the array
extent :: (Shape sh, Source r e) => Array r sh e -> sh
So, given a 3x3x3 array, of type Array U DIM3 Int, we can:
-- build an array
ghci> let x :: Array U DIM3 Int; x = fromListUnboxed (Z :. (3::Int) :. (3::Int) :. (3::Int)) [1..27]
ghci> :t x
x :: Array U DIM3 Int
-- query the extent
ghci> extent x
((Z :. 3) :. 3) :. 3
-- compute the rank (number of dimensions)
ghci> let sh = extent x
ghci> rank sh
3
-- compute the size (total number of elements)
> size sh
27
-- extract the elements of the array as a flat vector
ghci> toUnboxed x
fromList [1,2,3,4,5,6,7,8,9,10
,11,12,13,14,15,16,17,18,19
,20,21,22,23,24,25,26,27] :: Data.Vector.Unboxed.Base.Vector Int
Generating arrays
New repa arrays ("arrays" from here on) can be generated in many ways, and we always begin by importing the Data.Array.Repa module:
$ ghci
GHCi, version 7.4.1: http://www.haskell.org/ghc/ :? for help
Loading package ghc-prim ... linking ... done.
Loading package integer-gmp ... linking ... done.
Loading package base ... linking ... done.
ghci> :m + Data.Array.Repa
They may be constructed from lists, for example. Here is a one dimensional array of length 10, here, given the shape (Z :. 10):
ghci> let inputs = [1..10] :: [Double]
ghci> let x = fromListUnboxed (Z :. (10::Int)) inputs
ghci> x
AUnboxed (Z :. 10) (fromList [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0])
The type of x is inferred as:
ghci> :t x
x :: Array U (Z :. Int) Double
which we can read as "an array of dimension 1, indexed via Int keys, holding elements of type Double stored using unboxed vectors"
We could also have written the type as:
ghci> let x' = fromListUnboxed (Z :. 10 :: DIM1) inputs
ghci> :t x'
x' :: Array U DIM1 Double
The same data may also be treated as a two dimensional array, by changing the shape parameter:
ghci> let x2 = fromListUnboxed (Z :. (5::Int) :. (2::Int)) inputs
ghci> x2
AUnboxed ((Z :. 5) :. 2) (fromList [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0])
which has the type:
ghci> :t x2
x2 :: Array U ((Z :. Int) :. Int) Double
or, as above, if we define it with the type synonym for 2 dimensional Int- indexed arrays, DIM2:
ghci> let x2' = fromListUnboxed (Z :. 5 :. 2 :: DIM2) inputs
ghci> x2'
AUnboxed ((Z :. 5) :. 2) (fromList [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0])
ghci> :t x2'
x2' :: Array U DIM2 Double
Building arrays from vectors
It is also possible to build arrays from unboxed vectors, from the 'vector' package:
fromUnboxed :: (Shape sh, Unbox e) => sh -> Vector e -> Array U sh e
New arrays are built by applying a shape to the vector. For example:
ghci> :m + Data.Vector.Unboxed
ghci> let x = fromUnboxed (Z :. (10::Int)) (enumFromN 0 10)
ghci> x
AUnboxed (Z :. 10) (fromList [0.0,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0])
is a one-dimensional array of doubles. As usual, we can also impose other shapes:
ghci> let x = fromUnboxed (Z :. (3::Int) :. (3::Int)) (enumFromN 0 9)
ghci> x
AUnboxed ((Z :. 3) :. 3) (fromList [0.0,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0])
ghci> :t x
x :: Array U ((Z :. Int) :. Int) Double
to create a 3x3 array.
Generating random arrays
The repa-algorithms package lets us generate new arrays with random data:
-- 3d array of Ints, bounded between 0 and 255.
ghci> randomishIntArray (Z :. (3::Int) :. (3::Int) :. (3::Int)) 0 255 1
AUnboxed (((Z :. 3) :. 3) :. 3) (fromList [217,42,130,200,216,254,67,77,152,
85,140,226,179,71,23,17,152,84,47,17,45,5,88,245,107,214,136])
Reading arrays from files
Using the repa-io package, arrays may be written and read from files in a number of formats:
- as BMP files; and
- in a number of text formats.
with other formats rapidly appearing. An example: to write an 2D array to an ascii file:
ghci> :m +Data.Array.Repa.IO.Matrix
ghci> let x = fromList (Z :. 5 :. 2 :: DIM2) [1..10]
ghci> writeMatrixToTextFile "test.dat" x
This will result in a file containing:
MATRIX 5 2 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0
In turn, this file may be read back in via readMatrixFromTextFile.
ghci> xx <- readMatrixFromTextFile "test.dat"
ghci> xx
AUnboxed ((Z :. 5) :. 2) (fromList [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0])
ghci> :t xx
xx :: Array U DIM2 Double
To process .bmp files, use Data.Array.Repa.IO.BMP, as follows (currently reading only works for 24 bit .bmp):
Data.Array.Repa.IO.BMP> x <- readImageFromBMP "/tmp/test24.bmp"
Reads this .bmp image:

as a 3D array of Word8, which can be further processed.
For image IO in many, many formats, use the repa-devil library.
Copying arrays from pointers
You can also generate new repa arrays by copying data from a pointer. Here is an example, using fromForeignPtr:
import Data.Word
import Foreign.Ptr
import qualified Foreign.ForeignPtr.Safe as FPS
import qualified Data.Vector.Storable as V
import qualified Data.Array.Repa as R
import qualified Data.Array.Repa.Repr.ForeignPtr as RFP
import Data.Array.Repa
import Data.Array.Repa.IO.DevIL
i, j, k :: Int
(i, j, k) = (255, 255, 4) -- RGBA
-- 1D vector, filled with pretty colors
v :: V.Vector Word8
v = V.fromList . take (i * j * k) . cycle $ concat
[ [ r, g, b, 255 ]
| r <- [0 .. 255]
, g <- [0 .. 255]
, b <- [0 .. 255]
]
ptr2repa :: Ptr Word8 -> IO (R.Array RFP.F R.DIM3 Word8)
ptr2repa p = do
fp <- FPS.newForeignPtr_ p
return $ RFP.fromForeignPtr (Z :. i :. j :. k) fp
main = do
-- copy our 1d vector to a repa 3d array, via a pointer
r <- V.unsafeWith v ptr2repa
runIL $ writeImage "test.png" (RGBA r)
return ()
The v function creates a vector filled with pixel data (RGBA values); ptr2repa takes a Ptr, converts it to ForeignPtr which is then used to copy data into a 3D REPA array (first two dimensions correspond to pixel location, the third dimension corresponds to colour channel). In the main function we use unsafeWith function operating on storable vectors. It passes Ptr to vector's internal data to a function that operates on that Ptr (it may not modify the data). In our case this is the ptr2repa array, which returns image data wrapped in an array. That array is then passed as data to writeImage function. RGBA is a data constructor for Image type. This allows writeImage to interpret array data correctly. runIL is a wrapper around IO monad that guarantees that IL library will be properly initialized. The result is written to disk as this image:

Indexing arrays
To access elements in repa arrays, you provide an array and a shape, to access the element:
(!) :: (Shape sh, Source r e) => Array r sh e -> sh -> e
Indices start with 0. So:
ghci> let x = fromListUnboxed (Z :. (10::Int)) [1..10]
ghci> x ! (Z :. 2)
3.0
Note that we can't give just a bare literal as the shape, even for one-dimensional arrays:
> x ! 2
No instance for (Num (Z :. Int))
arising from the literal `2'
as the Z type isn't in the Num class, and Haskell's numeric literals are overloaded.
What if the index is out of bounds, though?
> x ! (Z :. 11)
*** Exception: ./Data/Vector/Generic.hs:244 ((!)): index out of bounds (11,10)
An exception is thrown. Older versions of repa offered safe indexing operator (!?) that returned Maybe, but it is no longer available in repa 3.2.
Operations on arrays
Besides indexing, there are many regular, list-like operations on arrays. Since many of the names parallel those in the Prelude, we import Repa qualified:
ghci> import qualified Data.Array.Repa as Repa
Maps, zips, filters and folds
Let us define an unboxed array:
ghci> let x = fromListUnboxed (Z :. (3::Int) :. (3::Int)) [1..9]
ghci> x
AUnboxed ((Z :. 3) :. 3) (fromList [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0])
We can map over multi-dimensional arrays with map, but since it conflicts with the definition in the Prelude, we have to use it with the qualifier we requested:
ghci> let y = Repa.map (^2) x
The type of Repa.map is:
map :: (Shape sh, Source r a) =>
(a -> b) -> Array r sh a -> Array D sh b
This means that result is a delayed array (represented by letter D in the return type). We can index into delayed array (remember that indices are 0-based):
ghci> y Repa.! (Z :. 0 :. 2)
9.0
ghci> y Repa.! (Z :. 2 :. 0)
49.0
Passing an incorrect index will NOT cause an exception:
ghci> y Repa.! (Z :. 0 :. 3)
16.0
ghci> y Repa.! (Z :. 0 :. -4)
0.0
ghci> y Repa.! (Z :. 10 :. 10)
0.0
Since delayed arrays are not instances of Show type class, we cannot display the whole array directly:
ghci> y
No instance for (Show (Array D ((Z :. Int) :. Int) Double))
arising from a use of `print'
To display y array it must be turned into manifest array by computing all its values. This can be done either with computeP, which evaluates array in parallel, or computeS, which evaluates values sequentially. Looking at the type of computeP:
ghci> :t computeP
computeP
:: (Monad m, Source r2 e, Load r1 sh e, Target r2 e) =>
Array r1 sh e -> m (Array r2 sh e)
we can see that the result is enclosed within a monad. The reason for this is that monads give a well defined notion of sequence and thus computeP enforces completion of parallel evaluation in a particular point of monadic computations. This prevents nested data parallelism, which is not supported by Repa. We don't really care here about monadic effect, so we can take the manifest array out of a monad after computeP is done:
ghci> computeP y :: IO (Array U DIM2 Double)
AUnboxed ((Z :. 3) :. 3) (fromList [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0])
ghci> z <- computeP y :: IO (Array U DIM2 Double)
ghci> z
AUnboxed ((Z :. 3) :. 3) (fromList [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0])
ghci> let [w] = computeP y :: [Array U DIM2 Double]
ghci> w
AUnboxed ((Z :. 3) :. 3) (fromList [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0])
Repa's map leaves the dimension unchanged:
ghci> extent x
(Z :. 3) :. 3
ghci> extent y
(Z :. 3) :. 3
There are four fold operations in Repa library: foldP, foldS, foldAllP and foldAllS. First two reduce the the inner dimension of the array, the last two reduce whole array to one value. The P and S suffixes stand for parallel and sequential evaluation. First parameter of parallel folds must be an associative sequential operator and the starting element must be a neutral element of that operator. This is required in order to ensure correctness of parallel evaluation.
Type of foldP is given as:
foldP :: (Monad m, Shape sh, Source r a, Unbox a, Elt a) =>
(a -> a -> a) -> a -> Array r (sh :. Int) a -> m (Array U sh a)
The x defined above was a 2D array:
ghci> extent x
(Z :. 3) :. 3
but if we sum each row:
ghci> Repa.foldP (+) 0 x
AUnboxed (Z :. 3) (fromList [6.0,15.0,24.0])
we get a 1D array instead (liftM is used to run extent function within a monad returned by foldP):
ghci> liftM extent (Repa.foldP (+) 0 x)
Z :. 3
Similarly, if y is a (3 x 3 x 2) 3D array:
ghci> let y = fromListUnboxed ((Z :. 3 :. 3 :. 2) :: DIM3) [1..18]
ghci> y
AUnboxed (((Z :. 3) :. 3) :. 2) (fromList [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0,11.0,12.0,13.0,14.0,15.0,16.0,17.0,18.0])
we can fold over the inner dimension:
ghci> Repa.foldP (+) 0 y
AUnboxed ((Z :. 3) :. 3) (fromList [3.0,7.0,11.0,15.0,19.0,23.0,27.0,31.0,35.0])
yielding a 2D (3 x 3) array in place of our 3D (3 x 3 x 3) array.
Two arrays may be combined via zipWith:
zipWith :: (Shape sh, Source r2 b, Source r1 a) =>
(a -> b -> c) -> Array r1 sh a -> Array r2 sh b -> Array D sh c
an example:
ghci> let y = Repa.zipWith (*) x x
ghci> computeP y :: IO (Array U DIM2 Double)
AUnboxed ((Z :. 3) :. 3) (fromList [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0])
ghci> extent y
(Z :. 3) :. 3
If the extent of the two array arguments differ, then the resulting array's extent is their intersection.
Mapping, with indices
A very powerful operator is traverse, an array transformation which also supplies the current index:
traverse :: (Shape sh', Shape sh, Source r a)
=> Array r sh a -- Source array
-> (sh -> sh') -- Function to produce the extent of the result.
-> ((sh -> a) -> sh' -> b) -- Function to produce elements of the result.
-- It is passed a lookup function to
-- get elements of the source.
-> Array D sh' b
This is quite a complicated type, because it is very general. Let's take it apart. The first argument is the source array, which is obvious. The second argument is a function that transforms the shape of the input array to yield the output array. So if the arrays are the same size, this function is id. It might grow or resize the shape in other ways.
Finally, the 3rd argument is where the magic is. It is a function (often anonymous one) that takes two parameters: a function that looks up elements of an original array and a location of the currently processed element in the new array. Based on these two parameters a new value is determined for the resulting array. Note that traverse goes through all elements of the resulting array and it is up to you how to get values of original array based on an index of the new array.
traverse returns a delayed array, which means we will use computeP to evaluate its values and display them on the screen.
So we see this generalizes map to support indexes, and optional inspection of the current element. Let's try some examples:
ghci> let x = fromListUnboxed (Z :. (3::Int) :. (3::Int) :. (3::Int)) [1..27] :: Array U DIM3 Int
ghci> x
AUnboxed (((Z :. 3) :. 3) :. 3) (fromList [1,2,3,4,5,6,7,8,9,
10,11,12,13,14,15,16,17,18,
19,20,21,22,23,24,25,26,27])
-- Keeping the shape the same, and just overwriting elements
-- Use `traverse` to set all elements to their `x` axis:
ghci> computeP $ traverse x id (\_ (Z :. i :. j :. k) -> i) :: IO (Array U DIM3 Int)
AUnboxed (((Z :. 3) :. 3) :. 3) (fromList [0,0,0,0,0,0,0,0,0,
1,1,1,1,1,1,1,1,1,
2,2,2,2,2,2,2,2,2])
-- Shuffle elements around, based on their index.
-- Rotate elements by swapping elements from rotated locations:
ghci> computeP $ traverse x id (\f (Z :. i :. j :. k) -> f (Z :. j :. k :. i)) :: IO (Array U DIM3 Int)
AUnboxed (((Z :. 3) :. 3) :. 3) (fromList [1,4,7,10,13,16,19,22,25,
2,5,8,11,14,17,20,23,26,
3,6,9,12,15,18,21,24,27])
-- Take a slice of one dimension. The resulting shape of the array changes
ghci> computeP $ traverse x (\(e :. _) -> e) (\f (Z :. i :. j) -> f (Z :. i :. j :. 0)) :: IO (Array U DIM2 Int)
AUnboxed ((Z :. 3) :. 3) (fromList [1,4,7,10,13,16,19,22,25])
The documentation on traverse provides further information.
Numeric operations: negation, addition, subtraction, multiplication
To perform basic numeric operations on Repa arrays you must use specialized operators: (+^) (addition), (-^) (subtraction), (*^) (multiplication) and (/^) (division). All these operators work element-wise and produce delayed arrays (they have to be computed if you want to have results as unboxed arrays).
ghci> let x = fromListUnboxed (Z :. (10 :: Int)) [1..10]
ghci> computeP $ x +^ x :: IO (Array U DIM1 Double)
AUnboxed (Z :. 10) (fromList [2.0,4.0,6.0,8.0,10.0,12.0,14.0,16.0,18.0,20.0])
ghci> computeP $ x -^ x :: IO (Array U DIM1 Double)
AUnboxed (Z :. 10) (fromList [0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0])
ghci> computeP $ x *^ x :: IO (Array U DIM1 Double)
AUnboxed (Z :. 10) (fromList [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0,100.0])
ghci> computeP $ x /^ x :: IO (Array U DIM1 Double)
AUnboxed (Z :. 10) (fromList [1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0])
Changing the shape of an array
One of the main advantages of repa-style arrays over other arrays in Haskell is the ability to reshape data without copying. This is achieved via *index-space transformations*.
An example: transposing a 2D array. First, the type of the transformation:
transpose2D :: (Source r e) => Array r DIM2 e -> Array D DIM2 e
Note that this transform will work on DIM2 arrays holding any elements. Now, to swap rows and columns, we have to modify the shape:
transpose2D a = backpermute (swap e) swap a
where
e = extent a
swap (Z :. i :. j) = Z :. j :. i
The swap function reorders the index space of the array. To do this, we extract the current shape of the array, and write a function that maps the index space from the old array to the new array. That index space function is then passed to backpermute which actually constructs the new array from the old one.
backpermute generates a new array from an old, when given the new shape, and a function that translates between the index space of each array (i.e. a shape transformer).
backpermute :: (Shape sh2, Shape sh1, Source r e) =>
sh2 -> (sh2 -> sh1) -> Array r sh1 e -> Array D sh2 e
Note that the array created is not actually evaluated (we only modified the index space of the array).
Transposition is such a common operation that it is provided by the library:
transpose :: (Shape sh, Source r e) =>
Array r ((sh :. Int) :. Int) e -> Array D ((sh :. Int) :. Int) e
The types indicate that it works on the lowest two dimensions of the array.
Arrays shape can be changed without altering the underlying data by using reshape:
ghci> let x = fromListUnboxed (Z :. (5 :: Int) :. (2 :: Int)) [1..10]
ghci> x
AUnboxed ((Z :. 5) :. 2) (fromList [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0])
ghci> computeP $ reshape (Z :. (2::Int) :. (5::Int)) x :: IO (Array U DIM2 Double)
AUnboxed ((Z :. 2) :. 5) (fromList [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0])
Examples
Following are some examples of useful functions that exercise the API.
Example: Rotating an image with backpermute
Flip an image upside down:
import Foreign.Ptr
import System.Environment
import Data.Word
import Data.Array.Repa hiding ((++))
import Data.Array.Repa.IO.DevIL
import Data.Array.Repa.Repr.ForeignPtr
main :: IO ()
main = do
[f] <- getArgs
(RGB v) <- runIL $ readImage f
rotated <- (computeP $ rot180 v) :: IO (Array F DIM3 Word8)
runIL $ writeImage ("flip-"++f) (RGB rotated)
rot180 :: (Source r e) => Array r DIM3 e -> Array D DIM3 e
rot180 g = backpermute e flop g
where
e@(Z :. x :. y :. _) = extent g
flop (Z :. i :. j :. k) =
(Z :. x - i - 1 :. y - j - 1 :. k)
Running this:
$ ghc -O2 --make -threaded -rtsopts repa.hs $ ./repa "haskell.jpg" +RTS -N2
Results in:

Example: matrix-matrix multiplication
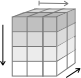
A more advanced example from the Repa paper is matrix-matrix multiplication. The result of matrix multiplication is a matrix whose elements are found by multiplying the elements of each row from the first matrix by the associated elements of the same column from the second matrix and summing the result.
if and
then
So we take two, 2D arrays and generate a new array, using our transpose function from earlier:
mmMult :: Monad m
=> Array U DIM2 Double
-> Array U DIM2 Double
-> m (Array U DIM2 Double)
mmMult a b = sumP (R.zipWith (*) aRepl bRepl)
where
t = transpose2D b
aRepl = extend (Z :.All :.colsB :.All) a
bRepl = extend (Z :.rowsA :.All :.All) t
(Z :.colsA :.rowsA) = extent a
(Z :.colsB :.rowsB) = extent b
The idea is to expand both 2D argument arrays into 3D arrays by
replicating them across a new axis using extend function. The front face of the cuboid that results represents the array a, which we replicate as often as b has columns (colsB), producing aRepl.
The top face represents t (the transposed b), which we
replicate as often as a has rows (rowsA), producing
bRepl,. The two replicated arrays have the same extent,
which corresponds to the index space of matrix multiplication.
Optimized implementations of this function are available in the repa-algorithms package.
Example: parallel image desaturation
To convert an image from color to greyscale, we can use the luminosity method to average RGB pixels into a common grey value, where the average is weighted for human perception of green.
The formula for luminosity is 0.21 R + 0.71 G + 0.07 B.
We can write a parallel image desaturation tool using repa and the repa-devil image library:
import Data.Array.Repa.IO.DevIL
import Data.Array.Repa hiding ((++))
import Data.Word
import System.Environment
--
-- Read an image, desaturate, write out with new name.
--
main = do
[f] <- getArgs
runIL $ do
a <- readImage f
let b = traverse a id luminosity
writeImage ("grey-" ++ f) b
And now the luminosity transform itself, which averages the 3 RGB colors based on perceived weight:
--
-- (Parallel) desaturation of an image via the luminosity method.
--
luminosity :: (DIM3 -> Word8) -> DIM3 -> Word8
luminosity _ (Z :. _ :. _ :. 3) = 255 -- alpha channel
luminosity f (Z :. i :. j :. _) = ceiling $ 0.21 * r + 0.71 * g + 0.07 * b
where
r = fromIntegral $ f (Z :. i :. j :. 0)
g = fromIntegral $ f (Z :. i :. j :. 1)
b = fromIntegral $ f (Z :. i :. j :. 2)
And that's it! The result is a parallel image desaturator, when compiled with
$ ghc -O -threaded -rtsopts --make A.hs -fforce-recomp
which we can run, to use two cores:
$ time ./A sunflower.png +RTS -N2 -H ./A sunflower.png +RTS -N2 -H 0.19s user 0.03s system 135% cpu 0.165 total
Given an image like this:

The desaturated result from Haskell:

Optimising Repa programs
Fusion, and why you need it
Repa depends critically on array fusion to achieve fast code. Fusion is a fancy name for the combination of inlining and code transformations performed by GHC when it compiles your program. The fusion process merges the array filling loops defined in the Repa library, with the "worker" functions that you write in your own module. If the fusion process fails, then the resulting program will be much slower than it needs to be, often 10x slower an equivalent program using plain Haskell lists. On the other hand, provided fusion works, the resulting code will run as fast as an equivalent cleanly written C program. Making fusion work is not hard once you understand what's going on.
The force function has the loops
Suppose we have the following binding:
arr' = R.force $ R.map (\x -> x + 1) arr
The right of this binding will compile down to code that first allocates the result array arr', then iterates over the source array arr, reading each element in turn and adding one to it, then writing to the corresponding element in the result.
Importantly, the code that does the allocation, iteration and update is defined as part of the force function. This forcing code has been written to break up the result into several chunks, and evaluate each chunk with a different thread. This is what makes your code run in parallel. If you do not use force then your code will be slow and not run in parallel.
Delayed and Manifest arrays
In the example from the previous section, think of the R.map (\x -> x + 1) arr expression as a specification for a new array. In the library, this specification is referred to as a delayed array. A delayed array is represented as a function that takes an array index, and computes the value of the element at that index.
Applying force to a delayed array causes all elements to be computed in parallel. The result of a force is referred to as a manifest array. A manifest array is a "real" array represented as a flat chunk of memory containing array elements.
All Repa array operators will accept both delayed and manifest arrays. However, if you index into a delayed array without forcing it first, then each indexing operation costs a function call. It also recomputes the value of the array element at that index.
Shells and Springs
Here is another way to think about Repa's approach to array fusion. Suppose we write the following binding:
arr' = R.force $ R.map (\x -> x * 2) $ R.map (\x -> x + 1) arr
Remember from the previous section, that the result of each of the applications of R.map is a delayed array. A delayed array is not a "real", manifest array, it's just a shell that contains a function to compute each element. In this example, the two worker functions correspond to the lambda expressions applied to R.map.
When GHC compiles this example, the two worker functions are fused into a fresh unfolding of the parallel loop defined in the code for R.force. Imagine holding R.force in your left hand, and squashing the calls to R.map into it, like a spring. Doing this breaks all the shells, and you end up with the worker functions fused into an unfolding of R.force.
INLINE worker functions
Consider the following example:
f x = x + 1 arr' = R.force $ R.zipWith (*) (R.map f arr1) (R.map f arr2)
During compilation, we need GHC to fuse our worker functions into a fresh unfolding of R.force. In this example, fusion includes inlining the definition of f. If f is not inlined, then the performance of the compiled code will be atrocious. It will perform a function call for each application of f, where it really only needs a single machine instruction to increment the x value.
Now, in general, GHC tries to avoid producing binaries that are "too big". Part of this is a heuristic that controls exactly what functions are inlined. The heuristic says that a function may be inlined only if it is used once, or if its definition is less than some particular size. If neither of these apply, then the function won't be inlined, killing performance.
For Repa programs, as fusion and inlining has such a dramatic effect on performance, we should absolutely not rely on heuristics to control whether or not this inlining takes place. If we rely on a heuristic, then even if our program runs fast today, if this heuristic is ever altered then some functions that used to be inlined may no longer be.
The moral of the story is to attach INLINE pragmas to all of your client functions that compute array values. This ensures that these critical functions will be inlined now, and forever.
{-# INLINE f #-}
f x = x + 1
arr' = R.force $ R.zipWith (*) (R.map f arr1) (R.map f arr2)
Advanced techniques
Repa's parallel programming model
Discussion about the gang threads and hooks to help
Programming with stencils
Discuss the stencil types model