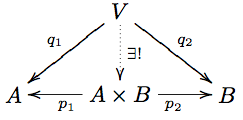Difference between revisions of "User:Michiexile/MATH198/Lecture 4"
Michiexile (talk | contribs) |
m |
||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ. |
||
| − | |||
===Product=== |
===Product=== |
||
| − | Recall the construction of a |
+ | Recall the construction of a cartesian product of two sets: <math>A\times B=\{(a,b) : a\in A, b\in B\}</math>. We have functions <math>p_A:A\times B\to A</math> and <math>p_B:A\times B\to B</math> extracting the two sets from the product, and we can take any two functions <math>f:A\to A'</math> and <math>g:B\to B'</math> and take them together to form a function <math>f\times g:A\times B\to A'\times B'</math>. |
| + | Similarly, we can form the type of pairs of Haskell types: <hask>Pair s t = (s,t)</hask>. For the pair type, we have canonical functions <hask>fst :: (s,t) -> s</hask> and <hask>snd :: (s,t) -> t</hask> extracting the components. And given two functions <hask>f :: s -> s'</hask> and <hask>g :: t -> t'</hask>, there is a function <hask>f *** g :: (s,t) -> (s',t')</hask>. |
||
| − | The cartesian product is one of the canonical ways to combine sets with each other. This is how we build binary operations, and higher ones - as well as how we formally define functions, partial functions and relations in the first place. |
||
| + | An element of the pair is completely determined by the two elements included in it. Hence, if we have a pair of generalized elements <math>q_1:V\to A</math> and <math>q_2:V\to B</math>, we can find a unique generalized element <math>q:V\to A\times B</math> such that the projection arrows on this gives us the original elements back. |
||
| − | This, too, is how we construct vector spaces: recall that <math>\mathbb R^n</math> is built out of tuples of elements from <math>\mathbb R</math>, with pointwise operations. This constructions reoccurs all over the place - sets with structure almost always have the structure carry over to products by pointwise operations. |
||
| + | This argument indicates to us a possible definition that avoids talking about elements in sets in the first place, and we are lead to the |
||
| − | The product of sets is determined by the projection maps <math>p_1:(s,t)\mapsto s</math> and <math>p_2: (s,t)\mapsto t</math>. You know any element of <math>S\times T</math> by knowing what its two coordinates are, and any element of <math>S</math> with an element of <math>T</math> determines exactly one element of <math>S\times T</math>. |
||
| + | '''Definition''' A ''product'' of two objects <math>A,B</math> in a category <math>C</math> is an object <math>A\times B</math> equipped with arrows <math>A \leftarrow^{p_1} A\times B\rightarrow^{p_2} B</math> such that for any other object <math>V</math> with arrows <math>A \leftarrow^{q_1} V \rightarrow^{q_2} B</math>, there is a unique arrow <math>V\to A\times B</math> such that the diagram |
||
| − | Given the cartesian product in sets, the important thing about the product is that we can extract both parts, and doing so preserves any structure present, since the structure is defined pointwise. |
||
| + | [[Image:AxBdiagram.png]] |
||
| − | This is what we use to define what we want to mean by products in a categorical setting. |
||
| + | commutes. The diagram <math>A \leftarrow^{p_1} A\times B\rightarrow^{p_2} B</math> is called a ''product cone'' if it is a diagram of a product with the ''projection arrows'' from its definition. |
||
| − | '''Definition''' Let <math>C</math> be a category. The ''product'' of two objects <math>A,B</math> is an object <math>A\times B</math> equipped with maps <math>p_1: A\times B\to A</math> and <math>p_2: A\times B\to B</math> such that any other object <math>V</math> with maps <math>A\leftarrow^{q_1} V\rightarrow^{q_2} B</math> has a unique map <math>V\to A\times B</math> such that both maps from <math>V</math> factor through the <math>p_1,p_2</math>. |
||
| − | In the category of |
+ | In the category of sets, the unique map is given by <math>q(v) = (q_1(v),q_2(v))</math>. In the Haskell category, it is given by the combinator <hask>(&&&) :: (a -> b) -> (a -> c) -> a -> (b,c)</hask>. |
| + | We tend to talk about ''the product''. The justification for this lies in the first interesting |
||
| − | The uniqueness requirement is what, in the theoretical setting, forces the product to be what we expect it to be - pairing of elements with no additional changes, preserving as much of the structure as we possibly can make it preserve. |
||
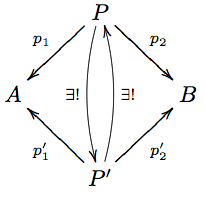
| + | '''Proposition''' If <math>P</math> and <math>P'</math> are both products for <math>A,B</math>, then they are isomorphic. |
||
| − | In the Haskell category, the product is simply the Pair type: |
||
| + | |||
| − | <haskell> |
||
| + | '''Proof''' Consider the diagram |
||
| − | Product a b = (a,b) |
||
| + | |||
| − | </haskell> |
||
| + | [[Image:ProductIsomorphismDiagram.png]] |
||
| − | and the projection maps <math>p_1,p_2</math> are just <hask>fst, snd</hask>. |
||
| + | |||
| + | Both vertical arrows are given by the product property of the two product cones involved. Their compositions are endo-arrows of <math>P, P'</math>, such that in each case, we get a diagram like |
||
| + | |||
| + | [[Image:AxBdiagram.png]] |
||
| + | with <math>V=A\times B=P</math> (or <math>P'</math>), and <math>q_1=p_1, q_2=p_2</math>. There is, by the product property, only one endoarrow that can make the diagram work - but both the composition of the two arrows, and the identity arrow itself, make the diagram commute. Therefore, the composition has to be the identity. QED. |
||
| − | Recall from the first lecture, the product construction on categories: objects are pairs of objects, morphisms are pairs of morphisms, identity morphisms are pairs of identity morphisms, and composition is componentwise. |
||
| + | We can expand the binary product to higher order products easily - instead of pairs of arrows, we have families of arrows, and all the diagrams carry over to the larger case. |
||
| − | This is, in fact, the product construction applied to <math>Cat</math> - or even to <math>CAT</math>: we get functors <math>P_1,P_2</math> picking out the first and second components, and everything works out exactly as in the cases above. |
||
| + | ====Binary functions==== |
||
| − | We keep writing ''the product'' here. The justification for this is: |
||
| − | '''Theorem''' If <math>P</math> and <math>P'</math> are both product objects for the pair <math>(A,B)</math>, then they are isomorphic. |
||
| + | Functions into a product help define the product in the first place, and function as elements of the product. Functions ''from'' a product, on the other hand, allow us to put a formalism around the idea of functions of several variables. |
||
| − | '''Proof''' Consider the diagram: |
||
| − | (( Diagram )) |
||
| − | Both the vertical maps have unique existence, by the defining property of the product. Hence the composition of these two maps, is an endo-map of <math>P</math> (<math>P'</math>) such that both projections factor through this endo-map. However, the identity map <math>1_P</math> (<math>1_{P'}</math>) is also such an endo-map, and again, by the definition of the product, a map to <math>P</math> (</math>P'</math>) that the projections factor through is uniquely determined. |
||
| − | Hence the composition is the identity, and this argument holds, mutatis mutandis, for the other inverse. Hence these vertical maps are isomorphisms, inverse to each other, and thus <math>P, P'</math> are isomorphic. QED. |
||
| + | So a function of two variables, of types <hask>A</hask> and <hask>B</hask> is a function <hask>f :: (A,B) -> C</hask>. The Haskell idiom for the same thing, <hask>A -> B -> C</hask> as a function taking one argument and returning a function of a single variable; as well as the <hask>curry</hask>/<hask>uncurry</hask> procedure is tightly connected to this viewpoint, and will reemerge below, as well as when we talk about adjunctions later on. |
||
===Coproduct=== |
===Coproduct=== |
||
| + | The product came, in part, out of considering the pair construction. One alternative way to write the <hask>Pair a b</hask> type is: |
||
| − | The other thing you can do in a Haskell data type declaration looks like this: |
||
<haskell> |
<haskell> |
||
| − | + | data Pair a b = Pair a b |
|
</haskell> |
</haskell> |
||
| − | and the |
+ | and the resulting type is isomorphic, in Hask, to the product type we discussed above. |
| + | This is one of two basic things we can do in a <hask>data</hask> type declaration, and corresponds to the ''record'' types in Computer Science jargon. |
||
| − | This type provides us with functions |
||
| + | |||
| + | The other thing we can do is to form a ''union'' type, by something like |
||
<haskell> |
<haskell> |
||
| − | + | data Union a b = Left a | Right b |
|
| − | B :: b -> Coproduct a b |
||
</haskell> |
</haskell> |
||
| + | which takes on either a value of type <hask>a</hask> or of type <hask>b</hask>, depending on what constructor we use. |
||
| − | and hence looks quite like a dual to the product construction, in that the guaranteed functions the type brings are in the reverse directions from the arrows that the product projection arrows. |
||
| + | This type guarantees the existence of two functions |
||
| − | So, maybe what we want to do is to simply dualize the entire definition? |
||
| + | <haskell> |
||
| + | Left :: a -> Union a b |
||
| + | Right :: b -> Union a b |
||
| + | </haskell> |
||
| + | Similarly, in the category of sets we have the disjoint union <math>S\coprod T = S\times 0 \cup T \times 1</math>, which also comes with functions <math>i_S: S\to S\coprod T, i_T: T\to S\coprod T</math>. |
||
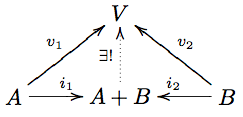
| − | '''Definition''' Let <math>C</math> be a category. The ''coproduct'' of two objects <math>A,B</math> is an object <math>A+B</math> equipped with maps <math>i_1:A\to A+B</math> and <math>i_2:B\to A+B</math> such that any other object <math>V</math> with maps <math>A\rightarrow_{v_1} V \leftarrow_{v_2} B</math> has a unique map <math>v:A+B\to V</math> such that <math>v_1 = v i_1</math> and <math>v_2 = v i_2</math>. |
||
| + | We can use all this to mimic the product definition. The directions of the inclusions indicate that we may well want the dualization of the definition. Thus we define: |
||
| − | In the Haskell case, the maps <math>i_1,i_2</math> are the type constructors <math>A, B</math>. And indeed, this Coproduct, the union type construction, is the type which guarantees inclusion of source types, but with minimal additional assumptions on the type. |
||
| + | '''Definition''' A ''coproduct'' <math>A+B</math> of objects <math>A, B</math> in a category <math>C</math> is an object equipped with arrows <math>A \rightarrow^{i_1} A+B \leftarrow^{i_2} B</math> such that for any other object <math>V</math> with arrows <math>A\rightarrow^{q_1} V\leftarrow^{q_2} B</math>, there is a unique arrow <math>A+B\to V</math> such that the diagram |
||
| − | In the category of sets, the coproduct construction is one where we can embed both sets into the coproduct, faithfully, and the result has no additional structure beyond that. Thus, the coproduct in set, is the disjoint union of the included sets: both sets are included without identifications made, and no extra elements are introduced. |
||
| + | [[Image:A-Bdiagram.png]] |
||
| − | '''Proposition''' If <math>C,C'</math> are both coproducts for some <math>A,B</math>, then they are isomorphic. |
||
| + | commutes. The diagram <math>A \rightarrow^{i_1} A+B \leftarrow^{i_2} B</math> is called a ''coproduct cocone'', and the arrows are ''inclusion arrows''. |
||
| − | The proof is almost exactly the same as the proof for the product case. |
||
| + | For sets, we need to insist that instead of just any <math>S\times 0</math> and <math>T\times 1</math>, we need the specific construction taking pairs for the coproduct to work out well. The issue here is that the categorical product is not defined as one single construction, but rather from how it behaves with respect to the arrows involved. |
||
| − | * Diagram definition |
||
| + | |||
| − | * Disjoint union in Set |
||
| + | With this caveat, however, the coproduct in Set really is the disjoint union sketched above. |
||
| − | * Coproduct of categories construction |
||
| + | |||
| − | * Union types |
||
| + | For Hask, the coproduct is the type construction of <hask>Union</hask> above - more usually written <hask>Either a b</hask>. |
||
| + | |||
| + | And following closely in the dualization of the things we did for products, there is a first |
||
| + | |||
| + | '''Proposition''' If <math>C, C'</math> are both coproducts for some pair <math>A, B</math> in a category <math>D</math>, then they are isomorphic. |
||
| + | |||
| + | The proof follows the exact pattern of the corresponding proposition for products. |
||
===Algebra of datatypes=== |
===Algebra of datatypes=== |
||
| − | Recall from [User:Michiexile/MATH198/Lecture_3|Lecture 3] that we can consider endofunctors as container datatypes. |
+ | Recall from [[User:Michiexile/MATH198/Lecture_3|Lecture 3]] that we can consider endofunctors as container datatypes. |
Some of the more obvious such container datatypes include: |
Some of the more obvious such container datatypes include: |
||
<haskell> |
<haskell> |
||
| Line 97: | Line 108: | ||
This allows us to start working out a calculus of data types with versatile expression power. We can produce recursive data type definitions by using equations to define data types, that then allow a direct translation back into Haskell data type definitions, such as: |
This allows us to start working out a calculus of data types with versatile expression power. We can produce recursive data type definitions by using equations to define data types, that then allow a direct translation back into Haskell data type definitions, such as: |
||
| + | |||
<math>List = 1 + T\times List</math> |
<math>List = 1 + T\times List</math> |
||
| + | |||
| − | <math>BinaryTree = T\times (1+BinaryTree\times BinaryTree)</math> |
||
| − | <math> |
+ | <math>BinaryTree = T+T\times BinaryTree\times BinaryTree</math> |
| + | |||
| − | <math>GenericTree = T\times (1+List\circ GenericTree)</math> |
||
| + | <math>TernaryTree = T+T\times TernaryTree\times TernaryTree\times TernaryTree</math> |
||
| + | |||
| + | <math>GenericTree = T+T\times (List\circ GenericTree)</math> |
||
The real power of this way of rewriting types comes in the recognition that we can use algebraic methods to reason about our data types. For instance: |
The real power of this way of rewriting types comes in the recognition that we can use algebraic methods to reason about our data types. For instance: |
||
| Line 114: | Line 129: | ||
<haskell> |
<haskell> |
||
| − | List = 1 + T * List -- and thus |
+ | List = 1 + T * List -- and thus |
| − | List - T * List = 1 -- even though (-) doesn't make sense for data types |
+ | List - T * List = 1 -- even though (-) doesn't make sense for data types |
| − | (1 - T) * List = 1 -- still ignoring that (-)... |
+ | (1 - T) * List = 1 -- still ignoring that (-)... |
| − | List = 1 / (1 - T) -- even though (/) doesn't make sense for data types |
+ | List = 1 / (1 - T) -- even though (/) doesn't make sense for data types |
= 1 + T + T*T + T*T*T + ... -- by the geometric series identity |
= 1 + T + T*T + T*T*T + ... -- by the geometric series identity |
||
</haskell> |
</haskell> |
||
| Line 124: | Line 139: | ||
At this point, I'd recommend anyone interested in more perspectives on this approach to data types, and thinks one may do with them, to read the following references: |
At this point, I'd recommend anyone interested in more perspectives on this approach to data types, and thinks one may do with them, to read the following references: |
||
| − | ====Blog posts==== |
+ | ====Blog posts and Wikipages==== |
| + | The ideas in this last section originate in a sequence of research papers from Conor McBride - however, these are research papers in logic, and thus come with all the quirks such research papers usually carry. Instead, the ideas have been described in several places by various blog authors from the Haskell community - which make for a more accessible but much less strict read. |
||
| − | ====Research papers==== |
||
| + | * http://en.wikibooks.org/wiki/Haskell/Zippers -- On zippers, and differentiating types |
||
| − | d for data types |
||
| + | * http://blog.lab49.com/archives/3011 -- On the polynomial data type calculus |
||
| − | 7 trees into 1 |
||
| + | * http://blog.lab49.com/archives/3027 -- On differentiating types and zippers |
||
| + | * http://comonad.com/reader/2008/generatingfunctorology/ -- Different recursive type constructions |
||
| + | * http://strictlypositive.org/slicing-jpgs/ -- Lecture slides for similar themes. |
||
| + | * http://blog.sigfpe.com/2009/09/finite-differences-of-types.html -- Finite differences of types - generalizing the differentiation approach. |
||
| + | * http://homepage.mac.com/sigfpe/Computing/fold.html -- Develops the underlying theory for our algebra of datatypes in some detail. |
||
===Homework=== |
===Homework=== |
||
| + | |||
| + | Complete points for this homework consists of 4 out of 5 exercises. Partial credit is given. |
||
# What are the products in the category <math>C(P)</math> of a poset <math>P</math>? What are the coproducts? |
# What are the products in the category <math>C(P)</math> of a poset <math>P</math>? What are the coproducts? |
||
# Prove that any two coproducts are isomorphic. |
# Prove that any two coproducts are isomorphic. |
||
| + | # Prove that any two exponentials are isomorphic. |
||
# Write down the type declaration for at least two of the example data types from the section of the algebra of datatypes, and write a <hask>Functor</hask> implementation for each. |
# Write down the type declaration for at least two of the example data types from the section of the algebra of datatypes, and write a <hask>Functor</hask> implementation for each. |
||
| + | # * Read up on Zippers and on differentiating data structures. Find the derivative of List, as defined above. Prove that <math>\partial List = List \times List</math>. Find the derivatives of BinaryTree, and of GenericTree. |
||
Latest revision as of 06:07, 22 October 2009
Product
Recall the construction of a cartesian product of two sets: . We have functions and extracting the two sets from the product, and we can take any two functions and and take them together to form a function .
Similarly, we can form the type of pairs of Haskell types: Pair s t = (s,t). For the pair type, we have canonical functions fst :: (s,t) -> s and snd :: (s,t) -> t extracting the components. And given two functions f :: s -> s' and g :: t -> t', there is a function f *** g :: (s,t) -> (s',t').
An element of the pair is completely determined by the two elements included in it. Hence, if we have a pair of generalized elements and , we can find a unique generalized element such that the projection arrows on this gives us the original elements back.
This argument indicates to us a possible definition that avoids talking about elements in sets in the first place, and we are lead to the
Definition A product of two objects in a category is an object equipped with arrows such that for any other object with arrows , there is a unique arrow such that the diagram
commutes. The diagram is called a product cone if it is a diagram of a product with the projection arrows from its definition.
In the category of sets, the unique map is given by . In the Haskell category, it is given by the combinator (&&&) :: (a -> b) -> (a -> c) -> a -> (b,c).
We tend to talk about the product. The justification for this lies in the first interesting
Proposition If and are both products for , then they are isomorphic.
Proof Consider the diagram
Both vertical arrows are given by the product property of the two product cones involved. Their compositions are endo-arrows of , such that in each case, we get a diagram like
with (or ), and . There is, by the product property, only one endoarrow that can make the diagram work - but both the composition of the two arrows, and the identity arrow itself, make the diagram commute. Therefore, the composition has to be the identity. QED.
We can expand the binary product to higher order products easily - instead of pairs of arrows, we have families of arrows, and all the diagrams carry over to the larger case.
Binary functions
Functions into a product help define the product in the first place, and function as elements of the product. Functions from a product, on the other hand, allow us to put a formalism around the idea of functions of several variables.
So a function of two variables, of types A and B is a function f :: (A,B) -> C. The Haskell idiom for the same thing, A -> B -> C as a function taking one argument and returning a function of a single variable; as well as the curry/uncurry procedure is tightly connected to this viewpoint, and will reemerge below, as well as when we talk about adjunctions later on.
Coproduct
The product came, in part, out of considering the pair construction. One alternative way to write the Pair a b type is:
data Pair a b = Pair a b
and the resulting type is isomorphic, in Hask, to the product type we discussed above.
This is one of two basic things we can do in a data type declaration, and corresponds to the record types in Computer Science jargon.
The other thing we can do is to form a union type, by something like
data Union a b = Left a | Right b
which takes on either a value of type a or of type b, depending on what constructor we use.
This type guarantees the existence of two functions
Left :: a -> Union a b
Right :: b -> Union a b
Similarly, in the category of sets we have the disjoint union , which also comes with functions .
We can use all this to mimic the product definition. The directions of the inclusions indicate that we may well want the dualization of the definition. Thus we define:
Definition A coproduct of objects in a category is an object equipped with arrows such that for any other object with arrows , there is a unique arrow such that the diagram
commutes. The diagram is called a coproduct cocone, and the arrows are inclusion arrows.
For sets, we need to insist that instead of just any and , we need the specific construction taking pairs for the coproduct to work out well. The issue here is that the categorical product is not defined as one single construction, but rather from how it behaves with respect to the arrows involved.
With this caveat, however, the coproduct in Set really is the disjoint union sketched above.
For Hask, the coproduct is the type construction of Union above - more usually written Either a b.
And following closely in the dualization of the things we did for products, there is a first
Proposition If are both coproducts for some pair in a category , then they are isomorphic.
The proof follows the exact pattern of the corresponding proposition for products.
Algebra of datatypes
Recall from Lecture 3 that we can consider endofunctors as container datatypes. Some of the more obvious such container datatypes include:
data 1 a = Empty
data T a = T a
These being the data type that has only one single element and the data type that has exactly one value contained.
Using these, we can generate a whole slew of further datatypes. First off, we can generate a data type with any finite number of elements by ( times). Remember that the coproduct construction for data types allows us to know which summand of the coproduct a given part is in, so the single elements in all the 1s in the definition of n here are all distinguishable, thus giving the final type the required number of elements.
Of note among these is the data type Bool = 2 - the Boolean data type, characterized by having exactly two elements.
Furthermore, we can note that , with the isomorphism given by the maps
f (Empty, T x) = T x
g (T x) = (Empty, T x)
Thus we have the capacity to add and multiply types with each other. We can verify, for any types
We can thus make sense of types like (either a triple of single values, or one out of two tagged pairs of single values).
This allows us to start working out a calculus of data types with versatile expression power. We can produce recursive data type definitions by using equations to define data types, that then allow a direct translation back into Haskell data type definitions, such as:
The real power of this way of rewriting types comes in the recognition that we can use algebraic methods to reason about our data types. For instance:
List = 1 + T * List
= 1 + T * (1 + T * List)
= 1 + T * 1 + T * T* List
= 1 + T + T * T * List
so a list is either empty, contains one element, or contains at least two elements. Using, though, ideas from the theory of power series, or from continued fractions, we can start analyzing the data types using steps on the way that seem completely bizarre, but arriving at important property. Again, an easy example for illustration:
List = 1 + T * List -- and thus
List - T * List = 1 -- even though (-) doesn't make sense for data types
(1 - T) * List = 1 -- still ignoring that (-)...
List = 1 / (1 - T) -- even though (/) doesn't make sense for data types
= 1 + T + T*T + T*T*T + ... -- by the geometric series identity
and hence, we can conclude - using formally algebraic steps in between - that a list by the given definition consists of either an empty list, a single value, a pair of values, three values, et.c.
At this point, I'd recommend anyone interested in more perspectives on this approach to data types, and thinks one may do with them, to read the following references:
Blog posts and Wikipages
The ideas in this last section originate in a sequence of research papers from Conor McBride - however, these are research papers in logic, and thus come with all the quirks such research papers usually carry. Instead, the ideas have been described in several places by various blog authors from the Haskell community - which make for a more accessible but much less strict read.
- http://en.wikibooks.org/wiki/Haskell/Zippers -- On zippers, and differentiating types
- http://blog.lab49.com/archives/3011 -- On the polynomial data type calculus
- http://blog.lab49.com/archives/3027 -- On differentiating types and zippers
- http://comonad.com/reader/2008/generatingfunctorology/ -- Different recursive type constructions
- http://strictlypositive.org/slicing-jpgs/ -- Lecture slides for similar themes.
- http://blog.sigfpe.com/2009/09/finite-differences-of-types.html -- Finite differences of types - generalizing the differentiation approach.
- http://homepage.mac.com/sigfpe/Computing/fold.html -- Develops the underlying theory for our algebra of datatypes in some detail.
Homework
Complete points for this homework consists of 4 out of 5 exercises. Partial credit is given.
- What are the products in the category of a poset ? What are the coproducts?
- Prove that any two coproducts are isomorphic.
- Prove that any two exponentials are isomorphic.
- Write down the type declaration for at least two of the example data types from the section of the algebra of datatypes, and write a
Functorimplementation for each. - * Read up on Zippers and on differentiating data structures. Find the derivative of List, as defined above. Prove that . Find the derivatives of BinaryTree, and of GenericTree.