Difference between revisions of "User:Michiexile/MATH198/Lecture 7"
Michiexile (talk | contribs) |
Michiexile (talk | contribs) |
||
| Line 57: | Line 57: | ||
We thus define a ''monad in a category <math>C</math>'' to be a monoid object in the category of endofunctors on that category. |
We thus define a ''monad in a category <math>C</math>'' to be a monoid object in the category of endofunctors on that category. |
||
| + | |||
| + | Specifically, this means: |
||
| + | |||
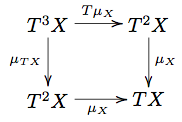
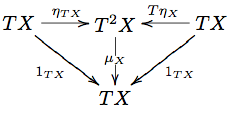
| + | '''Definition''' A ''monad'' in a category <math>C</math> is an endofunctor <math>T: C\to C</math> equipped with natural transformations <math>\mu: T^2\to T</math> and <math>\eta: 1\to T</math> such that the following diagrams commute: |
||
| + | |||
| + | [[Image:MonadAssociative.png]] |
||
| + | [[Image:MonadUnit.png]] |
||
We can take this definition and write it out in Haskell code, as: |
We can take this definition and write it out in Haskell code, as: |
||
| Line 91: | Line 98: | ||
which we recognize as the axioms of unity and associativity for the monad. |
which we recognize as the axioms of unity and associativity for the monad. |
||
| + | [[Image:MonadAssociative.png]] |
||
| − | (diagrams both here and above?) |
||
| + | [[Image:MonadUnit.png]] |
||
By working through the details of proving this to be an adjunction, and examining the resulting composition, it becomes clear that this is in fact the original monad <math>T</math>. However - while the Eilenberg-Moore construction is highly enlightening for constructing formal systems for algebraic theories, and even for the fixpoint definitions of data types, it is less enlightening to understand Haskell's monad definition. |
By working through the details of proving this to be an adjunction, and examining the resulting composition, it becomes clear that this is in fact the original monad <math>T</math>. However - while the Eilenberg-Moore construction is highly enlightening for constructing formal systems for algebraic theories, and even for the fixpoint definitions of data types, it is less enlightening to understand Haskell's monad definition. |
||
| Line 123: | Line 131: | ||
Hence, the composite <math>UF</math> really is just the original monad functor <math>T</math>. |
Hence, the composite <math>UF</math> really is just the original monad functor <math>T</math>. |
||
| − | But what's the big deal with this? you may ask. The big deal is that we now have a monad specification with a different signature. Indeed, the Kleisli arrow for an arrow <hask>f :: a -> b</hask> and a monad <hask>Monad m</hask> is something on the shape <hask>fk :: a -> m b</hask>. |
+ | But what's the big deal with this? you may ask. The big deal is that we now have a monad specification with a different signature. Indeed, the Kleisli arrow for an arrow <hask>f :: a -> b</hask> and a monad <hask>Monad m</hask> is something on the shape <hask>fk :: a -> m b</hask>. And the Kleisli factorization tells us that the Haskell monad specification and the Haskell monad laws are equivalent to their categorical counterparts. |
And the composition of Kleisli arrows is easy to write in Haskell: |
And the composition of Kleisli arrows is easy to write in Haskell: |
||
| Line 142: | Line 150: | ||
====The List monad==== |
====The List monad==== |
||
| − | Lists form a monad, with the following definition: |
+ | Lists form a monad, with the following (redundant) definition: |
<haskell> |
<haskell> |
||
instance Monad [] where |
instance Monad [] where |
||
| Line 154: | Line 162: | ||
</haskell> |
</haskell> |
||
| + | As it turns out, the lists monad can be found by considering the free and forgetful functors between sets and monoids. Indeed, the lists are what we get from the Kleene star operation, which is the monad we acquire by composing the free monoid functor with the forgetful functor. |
||
| + | ====Error handling==== |
||
| + | We can put a monadic structure on a coproduct <math>A+B</math> so that the monadic bind operation performs computations <math>A+B\to A'+B</math> until some computation fails, returning an error, typed <math>B</math>, after which we bypass any further computations, just carrying the error out of the entire computation. |
||
| + | The endofunctor here is <math>+B</math>. So the monad is given from a way to go from <math>A+B+B\to A+B</math>. Doing this is easy: in Haskell terms, we just remove the constructor differences between the two copies of <math>B</math> floating around. Mathematically, this is just using the functoriality of the coproduct construction on the inclusion maps into <math>A+B</math>. |
||
| + | For our example, we shall return the first value of <math>B</math> to ever occur, thus making our join operator look like this: |
||
| + | <haskell> |
||
| + | join :: (Either b (Either b a)) -> Either b a |
||
| + | join (Left y) = Left y |
||
| + | join (Right (Left y)) = Left y |
||
| + | join (Right (Right x)) = Right x |
||
| + | </haskell> |
||
| + | This gives us a Haskell monad defined by: |
||
| − | |||
<haskell> |
<haskell> |
||
| + | instance Monad (Either b) where |
||
| − | List: |
||
| − | return x = |
+ | return x = Right x |
| − | join (l:lsts) = l ++ join lsts |
||
| + | Left y >>= _ = Left y |
||
| − | Maybe: |
||
| − | + | Right x >>= f = f x |
|
| − | join (Just (Just x)) = Just x |
||
| − | join _ = Nothing |
||
</haskell> |
</haskell> |
||
| − | Note: not quite what Haskell claims a monad to be. Other related |
||
| − | concepts: |
||
| + | ===Additional reading=== |
||
| − | * Monads and sequencing. |
||
| + | * http://blog.sigfpe.com/2006/08/you-could-have-invented-monads-and.html (one of the least dramatic monads tutorials out there) |
||
| + | * http://www.disi.unige.it/person/MoggiE/ftp/lc88.ps.gz (Moggi: ''Computational lambda-calculus and monads'', one of the papers that started the interest in monads. Logic, dense reading.) |
||
| + | * http://www.haskell.org/haskellwiki/Research_papers/Monads_and_arrows (good catalogue over further reading on monads) |
||
| ⚫ | |||
| + | Full marks will be given for 4 out of the 7 questions. |
||
| − | |||
| − | |||
| − | |||
| − | |||
| ⚫ | |||
# Prove that the Kleisli category adjunction is an adjunction. |
# Prove that the Kleisli category adjunction is an adjunction. |
||
# Prove that the Eilenberg-Moore category adjunction is an adjunction. |
# Prove that the Eilenberg-Moore category adjunction is an adjunction. |
||
| + | # Given monad structures on <math>S</math> and <math>T</math>, |
||
# The ''writer'' monad <hask>W</hask> is defined by |
# The ''writer'' monad <hask>W</hask> is defined by |
||
#* <hask>data Monoid m => W m x = W (x, m)</hask> |
#* <hask>data Monoid m => W m x = W (x, m)</hask> |
||
| Line 194: | Line 209: | ||
## (2pt) Give the Kleisli factorization of the writer monad. |
## (2pt) Give the Kleisli factorization of the writer monad. |
||
## (2pt) Give the Eilenberg-Moore factorization of the writer monad. |
## (2pt) Give the Eilenberg-Moore factorization of the writer monad. |
||
| + | ## (2pt) Is there a nice, 'natural' adjunction factorizing the writer monad? |
||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ===Some adjunctions we already know=== |
||
| − | |||
| − | * initial/terminal are adjunctions. |
||
| − | * (co)-products are adjunctions. |
||
| − | * Actually, all (co)limits are adjunctions. |
||
| − | |||
| − | |||
| − | |||
| − | ===Some adjunctions we don't know yet=== |
||
| − | |||
| − | * Existential and universal qualifiers as adjunctions. |
||
| − | * Powersets and im(f) -| f^\inv |
||
| − | |||
| − | ===Properties of adjoints=== |
||
| − | |||
| − | ====RAPL: Right Adjoints Preserve Limits==== |
||
| − | |||
| − | ====Recognizing adjoints==== |
||
| − | |||
| − | '''Theorem''' (Freyd: The Adjoint Functor Theorem) |
||
| − | |||
| − | |||
| − | ===Why should we care in CS?=== |
||
| − | |||
| − | ====Monads==== |
||
Revision as of 18:40, 4 November 2009
IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ.
Last week we saw what an adjunction was. Here's one thing we can do with adjunctions.
Now, let be a left adjoint to . We set . Then we have natural transformations
such that is associative and is the unit of .
These requirements remind us of the definition of a monoid - and this is not that much of a surprise. To see the exact connection, and to garner a wider spread of definitions.
Algebraic objects in categories
We recall the definition of a monoid:
Definition A monoid is a set equipped with an operation that we call composition and an operation that we call the identity, such that
- (associativity)
- (unity)
If we have a monoidal category - a category with a bifunctor called the tensor product which is associative (up to natural isomorphisms) and has an object acting as a unit (up to natural isomorphisms) for the tensor product.
The product in a category certainly works as a tensor product, with a terminal object acting as a unit. However, there is often reason to have a non-commutative tensor product for the monoidal structure of a category. This makes the category a cartesian monoidal category.
For, say, abelian groups, or for vector spaces, we have the tensor product forming a non-cartesian monoidal category structure. And it is important that we do.
And for the category of endofunctors on a category, we have a monoidal structure induced by composition of endofunctors: . The unit is the identity functor.
Now, we can move the definition of a monoid out of the category of sets, and define a generic monoid object in a monoidal category:
Definition A monoid object in a monoidal category is an object equipped with morphisms and such that
- (associativity)
- (unity)
As an example, a monoid object in the cartesian monoidal category is just a monoid. A monoid object in the category of abelian groups is a ring.
A monoid object in the category of abelian groups, with the tensor product for the monoidal structure is a ring.
And the composition for an adjoint pair is a monoid object in the category of endofunctors on the category.
The same kind of construction can be made translating familiar algebraic definitions into categorical constructions with many different groups of definitions. For groups, the corresponding definition introduces a diagonal map , and an inversion map to codify the entire definition.
One framework that formalizes the whole thing, in such a way that the definitions themselves form a category is the theory of Sketches by Charles Wells. In one formulation we get the following definition:
Definition A sketch consists of a graph , a set of diagrams , a set of cones in and a set of cocones in .
A model of a sketch S in a category is a graph homomorphism such that the image of each diagram in is commutative, each of the cones is a limit cone and each of the cocones is a colimit cocone.
A homomorphism of models is just a natural transformation between the models.
We thus define a monad in a category to be a monoid object in the category of endofunctors on that category.
Specifically, this means:
Definition A monad in a category is an endofunctor equipped with natural transformations and such that the following diagrams commute:
We can take this definition and write it out in Haskell code, as:
class Functor m => MathematicalMonad m where
return :: a -> m a
join :: m (m a) -> m a
-- such that
join . fmap return = id :: m a -> m a
join . return = id :: m a -> m a
join . join = join . fmap join :: m (m (m a)) -> m a
Those of you used to Haskell will notice that this is not the same as the Monad typeclass. That type class calls for a natural transformation (>>=) :: m a -> (a -> m b) -> m b (or bind).
The secret of the connection between the two lies in the Kleisli category, and a way to build adjunctions out of monads as well as monads out of adjunctions.
Kleisli category
We know that an adjoint pair will give us a monad. But what about getting an adjoint pair out of a monad? Can we reverse the process that got us the monad in the first place?
There are several different ways to do this. Awodey uses the Eilenberg-Moore category which has as objects the algebras of the monad : morphisms . A morphism is just some morphism in the category such that .
We require of -algebras two additional conditions:
- (unity)
- (associativity)
There is a forgetful functor that takes some to , picking up the object of the -algebra. Thus , and .
We shall construct a left adjoint to this from the data of the monad by setting , making the corresponding object. And plugging the corresponding data into the equations, we get:
which we recognize as the axioms of unity and associativity for the monad.
By working through the details of proving this to be an adjunction, and examining the resulting composition, it becomes clear that this is in fact the original monad . However - while the Eilenberg-Moore construction is highly enlightening for constructing formal systems for algebraic theories, and even for the fixpoint definitions of data types, it is less enlightening to understand Haskell's monad definition.
To get to terms with the Haskell approach, we instead look to a different construction aiming to fulfill the same aim: the Kleisli category:
Given a monad over a category , equipped with unit and concatenation , we shall construct a new category , and an adjoint pair of functors factorizing the monad into .
We first define , keeping the objects from the original category.
Then, we set to be the collection of arrows, in , on the form .
The composition of with is given by the sequence
The identity is the arrow . The identity property follows directly from the unity axiom for the monad, since composing with is the identity.
Given this category, we next define the functors:
This definition makes an adjoint pair. Furthermore, we get
- , and by naturality of , we can rewrite this as
- by unitality of .
Hence, the composite really is just the original monad functor .
But what's the big deal with this? you may ask. The big deal is that we now have a monad specification with a different signature. Indeed, the Kleisli arrow for an arrow f :: a -> b and a monad Monad m is something on the shape fk :: a -> m b. And the Kleisli factorization tells us that the Haskell monad specification and the Haskell monad laws are equivalent to their categorical counterparts.
And the composition of Kleisli arrows is easy to write in Haskell:
f :: a -> m b
g :: b -> m c
(>>=) :: m a -> (a -> m b) -> m b -- Monadic bind, the Haskell definition
kleisliCompose f g :: a -> m c
kleisliCompose f g = (>>= g) . f
Examples
Some monads in Haskell are:
The List monad
Lists form a monad, with the following (redundant) definition:
instance Monad [] where
return x = [x]
[] >>= _ = []
(x:xs) >>= f = f x : xs >>= f
join [] = []
join (l:ls) = l ++ join ls
As it turns out, the lists monad can be found by considering the free and forgetful functors between sets and monoids. Indeed, the lists are what we get from the Kleene star operation, which is the monad we acquire by composing the free monoid functor with the forgetful functor.
Error handling
We can put a monadic structure on a coproduct so that the monadic bind operation performs computations until some computation fails, returning an error, typed , after which we bypass any further computations, just carrying the error out of the entire computation.
The endofunctor here is . So the monad is given from a way to go from . Doing this is easy: in Haskell terms, we just remove the constructor differences between the two copies of floating around. Mathematically, this is just using the functoriality of the coproduct construction on the inclusion maps into .
For our example, we shall return the first value of to ever occur, thus making our join operator look like this:
join :: (Either b (Either b a)) -> Either b a
join (Left y) = Left y
join (Right (Left y)) = Left y
join (Right (Right x)) = Right x
This gives us a Haskell monad defined by:
instance Monad (Either b) where
return x = Right x
Left y >>= _ = Left y
Right x >>= f = f x
Additional reading
- http://blog.sigfpe.com/2006/08/you-could-have-invented-monads-and.html (one of the least dramatic monads tutorials out there)
- http://www.disi.unige.it/person/MoggiE/ftp/lc88.ps.gz (Moggi: Computational lambda-calculus and monads, one of the papers that started the interest in monads. Logic, dense reading.)
- http://www.haskell.org/haskellwiki/Research_papers/Monads_and_arrows (good catalogue over further reading on monads)
Homework
Full marks will be given for 4 out of the 7 questions.
- Prove that the Kleisli category adjunction is an adjunction.
- Prove that the Eilenberg-Moore category adjunction is an adjunction.
- Given monad structures on and ,
- The writer monad
Wis defined bydata Monoid m => W m x = W (x, m)fmap f (W (x, m)) = W (f x, m) #* <hask>return x = W (x, mempty)join (W (W (x, m), n)) = W (x, m `mappend` n)
- (2pt) Prove that this yields a monad.
- (2pt) Give the Kleisli factorization of the writer monad.
- (2pt) Give the Eilenberg-Moore factorization of the writer monad.
- (2pt) Is there a nice, 'natural' adjunction factorizing the writer monad?