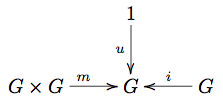Difference between revisions of "User:Michiexile/MATH198/Lecture 8"
Michiexile (talk | contribs) |
Michiexile (talk | contribs) |
||
| Line 1: | Line 1: | ||
IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ. |
IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ. |
||
| − | ===Some adjunctions we already know=== |
||
| + | ===Algebras over monads=== |
||
| − | * initial/terminal are adjunctions. |
||
| − | * (co)-products are adjunctions. |
||
| − | * Actually, all (co)limits are adjunctions. |
||
| + | We recall from the last lecture the definition of an Eilenberg-Moore algebra over a monad <math>T = (T, \eta, \mu)</math>: |
||
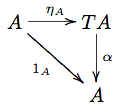
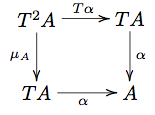
| + | '''Definition''' An ''algebra'' over a monad <math>T</math> in a category <math>C</math> (a <math>T</math>-algebra) is a morphism <math>\alpha\in C(TA, A)</math>, such that the diagrams below both commute: |
||
| + | [[Image:EilenbergMooreUnity.png]] |
||
| − | ===Some adjunctions we don't know yet=== |
||
| + | [[Image:EilenbergMooreAssociativity.png]] |
||
| + | While a monad corresponds to the imposition of some structure on the objects in a category, an algebra over that monad corresponds to some evaluation of that structure. |
||
| − | * Existential and universal qualifiers as adjunctions. |
||
| − | * Powersets and im(f) -| f^\inv |
||
| − | === |
+ | ====Example: monoids==== |
| + | Let <math>T</math> be the Kleene star monad - the one we get from the adjunction of free and forgetful functors between Monoids and Sets. Then a <math>T</math>-algebra on a set <math>A</math> is equivalent to a monoid structure on <math>A</math>. |
||
| − | ====RAPL: Right Adjoints Preserve Limits==== |
||
| + | Indeed, if we have a monoid structure on <math>A</math>, given by <math>m:A^2\to A</math> and <math>u:1\to A</math>, we can construct a <math>T</math>-algebra by |
||
| − | ====Recognizing adjoints==== |
||
| + | :<math>\alpha([]) = u</math> |
||
| + | :<math>\alpha([a_1,a_2,\dots,a_n]) = m(a_1,\alpha([a_2,\dots,a_n]))</math> |
||
| + | This gives us, indeed, a <math>T<math>-algebra structure on <math>A</math>. Associativity and unity follows from the corresponding properties in the monoid. |
||
| + | On the other hand, if we have a <math>T</math>-algebra structure on <math>A</math>, we can construct a monoid structure by setting |
||
| − | '''Theorem''' (Freyd: The Adjoint Functor Theorem) |
||
| + | :<math>u = \alpha([])</math> |
||
| + | :<math>m(a,b) = \alpha([a,b])</math> |
||
| + | It is clear that associativity of <math>m</math> follows from the associativity of <math>\alpha</math>, and unitality of <math>u</math> follows from the unitality of <math>\alpha</math>. |
||
| + | (((potential headache: shouldn't <math>\eta</math> show up more? Instead of the empty list, maybe?))) |
||
| − | ===Yoneda's Lemma=== |
||
| + | ====Example: Vector spaces==== |
||
| − | ===F-functors and algebraic data structures=== |
||
| + | |||
| + | We have free and forgetful functors |
||
| + | :<math>Set \to^{free} k-Vect \to^{forgetful} Set</math> |
||
| + | forming an adjoint pair; where the free functor takes a set <math>S</math> and returns the vector space with basis <math>S</math>; while the forgetful functor takes a vector space and returns the set of all its elements. |
||
| + | |||
| + | The composition of these yields a monad <math>T</math> in <math>Set</math> taking a set <math>S</math> to the set of all formal linear combinations of elements in <math>S</math>. The monad multiplication takes formal linear combinations of formal linear combinations and multiplies them out: |
||
| + | :<math>3(2v+5w)-5(3v+2w) = 6v+15w-15v-10w = -9v+5w</math> |
||
| + | |||
| + | A <math>T</math>-algebra is a map <math>\alpha: TA\to A</math> that ''acts like a vector space'' in the sense that <math>\alpha(\sum\alpha_i(\sum\beta_jv_j)) = \alpha(\sum\alpha_i\beta_jv_j)</math>. |
||
| + | |||
| + | We can define <math>\lambda\cdot v = \alpha(\lambda v)</math> and <math>v+w=\alpha(v+w)</math>. The operations thus defined are associative, distributive, commutative, and everything else we could wish for in order to define a vector space - precisely because the operations inside <math>TA</math> are, and <math>\alpha</math> is associative. |
||
| + | |||
| + | ---- |
||
| + | |||
| + | The moral behind these examples is that using monads and monad algebras, we have significant power in defining and studying algebraic structures with categorical and algebraic tools. This paradigm ties in closely with the theory of ''operads'' - which has its origins in topology, but has come to good use within certain branches of universal algebra. |
||
| + | |||
| + | An (non-symmetric) ''operad'' is a graded set <math>O = \bigoplus_i O_i</math> equipped with composition operations <math>\circ_i: O_n\oplus O_m\to O_{n+m-1}</math> that obey certain unity and associativity conditions. As it turns out, non-symmetric operads correspond to the summands in a monad with polynomial underlying functor, and from a non-symmetric operad we can construct a corresponding monad. |
||
| + | |||
| + | The designator non-symmetric floats in this text o avoid dealing with the slightly more general theory of symmetric operads - which allow us to resort the input arguments, thus including the symmetrizer of a symmetric monoidal category in the entire definition. |
||
| + | |||
| + | To read more about these correspondences, I can recommend you start with: the blog posts ''Monads in Mathematics'' here: |
||
| + | [http://embuchestissues.wordpress.com/tag/monads-in-mathematics/] |
||
| + | |||
| + | |||
| + | ===Algebras over endofunctors=== |
||
| + | |||
| + | Suppose we started out with an endofunctor that is not the underlying functor of a monad - or an endofunctor for which we don't want to settle on a monadic structure. We can still do a lot of the Eilenberg-Moore machinery on this endofunctor - but we don't get quite the power of algebraic specification that monads offer us. At the core, here, lies the lack of associativity for a generic endofunctor - and algebras over endofunctors, once defined, will correspond to non-associative correspondences to their monadic counterparts. |
||
| + | |||
| + | '''Definition''' For an endofunctor <math>P:C\to C</math>, we define a ''<math>P</math>-algebra'' to be an arrow <math>\alpha\in C(PA,A)</math>. |
||
| + | |||
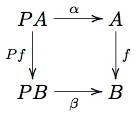
| + | A homomorphism of <math>P</math>-algebras <math>\alpha\to\beta</math> is some arrow <math>f:A\to B</math> such that the diagram below commutes: |
||
| + | :[[Image:EilenbergMoorePMorphism.png]] |
||
| + | |||
| + | This homomorphism definition does not need much work to apply to the monadic case as well. |
||
| + | |||
| + | ====Example: Groups==== |
||
| + | |||
| + | A group is a set <math>G</math> with operations <math>u: 1\to G, i: G\to G, m: G\times G\to G</math>, such that <math>u</math> is a unit for <math>m</math>, <math>m</math> is associative, and <math>i</math> is an inverse. |
||
| + | |||
| + | Ignoring for a moment the properties, the theory of groups is captured by these three maps, or by a diagram |
||
| + | :[[Image:GroupDiagram.png]] |
||
| + | |||
| + | |||
| + | |||
| + | ===Homework=== |
||
| + | |||
| + | # Find a monad whose algebras are ''associative algebras'': vector spaces with a binary, associative, unitary operation (multiplication) defined on them. Factorize the monad into a free/forgetful adjoint pair. |
||
| + | # Find an endofunctor of <math>Hask</math> whose initial object describes trees that are either binary of ternary at each point, carrying values from some <math>A</math> in the leaves. |
||
| + | # Write an implementation of the monad of vector spaces in Haskell. If this is tricky, restrict the domain of the monad to, say, a 3-element set, and implement the specific example of a 3-dimensional vector space as a monad. Hint: [http://sigfpe.blogspot.com] has written about this approach. |
||
Revision as of 17:33, 10 November 2009
IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ.
Algebras over monads
We recall from the last lecture the definition of an Eilenberg-Moore algebra over a monad :
Definition An algebra over a monad in a category (a -algebra) is a morphism , such that the diagrams below both commute:
While a monad corresponds to the imposition of some structure on the objects in a category, an algebra over that monad corresponds to some evaluation of that structure.
Example: monoids
Let be the Kleene star monad - the one we get from the adjunction of free and forgetful functors between Monoids and Sets. Then a -algebra on a set is equivalent to a monoid structure on .
Indeed, if we have a monoid structure on , given by and , we can construct a -algebra by
This gives us, indeed, a . Associativity and unity follows from the corresponding properties in the monoid.
On the other hand, if we have a -algebra structure on , we can construct a monoid structure by setting
It is clear that associativity of follows from the associativity of , and unitality of follows from the unitality of .
(((potential headache: shouldn't show up more? Instead of the empty list, maybe?)))
Example: Vector spaces
We have free and forgetful functors
forming an adjoint pair; where the free functor takes a set and returns the vector space with basis ; while the forgetful functor takes a vector space and returns the set of all its elements.
The composition of these yields a monad in taking a set to the set of all formal linear combinations of elements in . The monad multiplication takes formal linear combinations of formal linear combinations and multiplies them out:
A -algebra is a map that acts like a vector space in the sense that .
We can define and . The operations thus defined are associative, distributive, commutative, and everything else we could wish for in order to define a vector space - precisely because the operations inside are, and is associative.
The moral behind these examples is that using monads and monad algebras, we have significant power in defining and studying algebraic structures with categorical and algebraic tools. This paradigm ties in closely with the theory of operads - which has its origins in topology, but has come to good use within certain branches of universal algebra.
An (non-symmetric) operad is a graded set equipped with composition operations that obey certain unity and associativity conditions. As it turns out, non-symmetric operads correspond to the summands in a monad with polynomial underlying functor, and from a non-symmetric operad we can construct a corresponding monad.
The designator non-symmetric floats in this text o avoid dealing with the slightly more general theory of symmetric operads - which allow us to resort the input arguments, thus including the symmetrizer of a symmetric monoidal category in the entire definition.
To read more about these correspondences, I can recommend you start with: the blog posts Monads in Mathematics here: [1]
Algebras over endofunctors
Suppose we started out with an endofunctor that is not the underlying functor of a monad - or an endofunctor for which we don't want to settle on a monadic structure. We can still do a lot of the Eilenberg-Moore machinery on this endofunctor - but we don't get quite the power of algebraic specification that monads offer us. At the core, here, lies the lack of associativity for a generic endofunctor - and algebras over endofunctors, once defined, will correspond to non-associative correspondences to their monadic counterparts.
Definition For an endofunctor , we define a -algebra to be an arrow .
A homomorphism of -algebras is some arrow such that the diagram below commutes:
This homomorphism definition does not need much work to apply to the monadic case as well.
Example: Groups
A group is a set with operations , such that is a unit for , is associative, and is an inverse.
Ignoring for a moment the properties, the theory of groups is captured by these three maps, or by a diagram
Homework
- Find a monad whose algebras are associative algebras: vector spaces with a binary, associative, unitary operation (multiplication) defined on them. Factorize the monad into a free/forgetful adjoint pair.
- Find an endofunctor of whose initial object describes trees that are either binary of ternary at each point, carrying values from some in the leaves.
- Write an implementation of the monad of vector spaces in Haskell. If this is tricky, restrict the domain of the monad to, say, a 3-element set, and implement the specific example of a 3-dimensional vector space as a monad. Hint: [2] has written about this approach.