Difference between revisions of "Zipper"
EndreyMark (talk | contribs) m (better intro for a sentence) |
EndreyMark (talk | contribs) (→Comonads and monads: related external links (Tarmo Uustalu's papers and an article from A Neighborhood of Infinity)) |
||
| Line 171: | Line 171: | ||
in the existing Haskell. |
in the existing Haskell. |
||
[http://pobox.com/~oleg/ftp/Computation/Continuations.html#zipper Generic Zipper and its applications] |
[http://pobox.com/~oleg/ftp/Computation/Continuations.html#zipper Generic Zipper and its applications] |
||
| + | |||
| + | == Comonads and monads == |
||
| + | |||
| + | Comonads |
||
| + | * [http://cs.ioc.ee/~tarmo/tsem05/uustalu0812-slides.pdf Structured Computation on Trees or, What’s Behind That Zipper? (A Comonad)], slides by Tarmo Uustalu |
||
| + | * [http://cs.ioc.ee/~tarmo/papers/tfp05-book.pdf Comonadic functional attribute evaluation] by Tarmo Uustalu1 and Varmo Vene, a more detailed treatment |
||
| + | * [http://www.cs.nott.ac.uk/~txa/monads-more-4.pdf Monads and more (Part 4)] by Tarmo Uustalu |
||
| + | Monads: |
||
| + | * [http://sigfpe.blogspot.com/2007/01/monads-hidden-behind-every-zipper.html The Monads Hidden Behind Every Zipper], part of Sigfpe's ''A Neighborhood of Infinity'' |
||
| + | |||
== Applications == |
== Applications == |
||
Revision as of 13:53, 17 July 2007
The Zipper is an idiom that uses the idea of "context" to the means of manipulating locations in a data structure. Zipper monad is a monad which implements the zipper for binary trees.
Sometimes you want to manipulate a location inside a data structure, rather than the data itself. For example, consider a simple binary tree type:
data Tree a = Fork (Tree a) (Tree a) | Leaf a
and a sample tree t:
t = Fork (Fork (Leaf 1)
(Leaf 2))
(Fork (Leaf 3)
(Leaf 4))
|

|
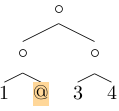
Each subtree of this tree occupies a certain location in the tree taken as a whole. The location consists of the subtree, along with the rest of the tree, which we think of the context of that subtree. For example, the context of
Leaf 2
in the above tree is
Fork (Fork (Leaf 1) @)
(Fork (Leaf 3) (Leaf 4))
|
|
where @ marks the focus: the spot that the subtree appears in. One way of expressing this context is as a path from the root of the tree to the required subtree. To reach our subtree, we needed to go down the left branch, and then down the right one. Note that the context is essentially a way of representing the tree, "missing out" a subtree (the subtree we are interested in). (A naive implementation inspired directly by the graphical representation — using Tree (Maybe a) instead of Tree (Maybe a) — would lose an essential point: the focus is unique.)
We can represent a context as follows:
data Cxt a = Top | L (Cxt a) (Tree a) | R (Tree a) (Cxt a)
L c t represents the left part of a branch of which the right part was t and whose parent had context c. The R constructor is similar. Top represents the top of a tree.
Remarks:
- In fact, this is equivalent to a list, whose elements are the appropriate collateral trees, each element labeled with the information which direction was chosen:
type Context a = [(Direction, Tree a)]data Direction = Lft | Rght- In both representations, we propagate from the focus towards the root.
- Note that in the original paper, Huet dealt with B-trees (ones where nodes have arbitrary numbers of branches), so lists are used instead of the (Tree a) parameters.
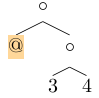
Using this datatype, we can rewrite the sample context above in proper Haskell:
R (Leaf 1) (L Top (Fork (Leaf 3) (Leaf 4)))
Note that the context is actually written by giving the path from the subtree to the root (rather than the other way round):

| ||
| ||
| Top |
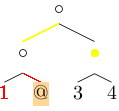
Or the more deconstructed representation:
|
where , are the appropriate correspondents of the , of the previous image. It is the empty list that represents .
Now we can define a tree location:
type Loc a = (Tree a, Cxt a)
and some useful functions for manipulating locations in a tree:
left :: Loc a -> Loc a
left (Fork l r, c) = (l, L c r)
right :: Loc a -> Loc a
right (Fork l r, c) = (r, R l c)
top :: Tree a -> Loc a
top t = (t, Top)
up :: Loc a -> Loc a
up (t, L c r) = (Fork t r, c)
up (t, R l c) = (Fork l t, c)
upmost :: Loc a -> Loc a
upmost l@(t, Top) = l
upmost l = upmost (up l)
modify :: Loc a -> (Tree a -> Tree a) -> Loc a
modify (t, c) f = (f t, c)
It is instructive to look at an example of how a location gets transformed as we move from root to leaf. Recall our sample tree t. Let's name some of the relevant subtrees for brevity:
t = let tl = Fork (Leaf 1) (Leaf 2)
tr = Fork (Leaf 3) (Leaf 4)
in Fork tl tr
Then to reach the location of Leaf 2:
(right . left . top) t
= (right . left) (t, Top)
= right (tl, L Top tr)
= (Leaf 2, R (Leaf 1) (L Top tr))
To reach that location and replace Leaf 2 by Leaf 0:
modify ((right . left . top) t) (\_ -> Leaf 0)
= ...
= (Leaf 0, R (Leaf 1) (L Top tr))
Afterwards some may like to continue walking to other parts of the new tree, in which case continue applying left, right, and up.
Some others may like to retrieve the new tree (and possibly forget about locations), in which case upmost is useful:
(fst . upmost) (modify ((right . left . top) t) (\_ -> Leaf 0))
= (fst . upmost) (Leaf 0, R (Leaf 1) (L Top tr))
= fst (Fork (Fork (Leaf 1)
(Leaf 0))
tr
, Top)
= Fork (Fork (Leaf 1)
(Leaf 0))
tr
Automation
There's a principled way to get the necessary types for contexts and the context filling functions, namely by differentiating the data structure. Some relevant papers.
For an actual implementation in Generic Haskell, see the paper Type-indexed data types by Ralf Hinze, Johan Jeuring and Andres Löh.
Alternative formulation
The dual of Huet zipper is generic zipper -- which is a derivative of a traversal function rather than that of a data structure. Unlike Huet zipper, generic zipper can be implemented once and for all data structures, in the existing Haskell. Generic Zipper and its applications
Comonads and monads
Comonads
- Structured Computation on Trees or, What’s Behind That Zipper? (A Comonad), slides by Tarmo Uustalu
- Comonadic functional attribute evaluation by Tarmo Uustalu1 and Varmo Vene, a more detailed treatment
- Monads and more (Part 4) by Tarmo Uustalu
Monads:
- The Monads Hidden Behind Every Zipper, part of Sigfpe's A Neighborhood of Infinity
Applications
- ZipperFS
- Oleg Kiselyov's zipper-based file server/OS where threading and exceptions are all realized via delimited continuations.
- Roll Your Own Window Manager: Tracking Focus with a Zipper
- describes the use of zippers in xmonad.
Further reading
- Gerard Huet's paper where he originally proposed the concept of a zipper
- The Web extends this pattern.
- Infinitesimal Types writes on interesting generalizations (e.g. derivative of a type — to the analogy of the notion of derivative in rings, e.g. in analysis or for polinomials)
- Haskell/Zippers on Wikibooks, a detailed treatment of zippers, and generalizing the notion as derivative
- Generic Zipper and its applications, writing that "Zipper can be viewed as a delimited continuation reified as a data structure" (link added).