Arrows are a new abstract view of computation, defined by John Hughes [Hug00]. They serve much the same purpose as monads -- providing a common structure for libraries -- but are more general. In particular they allow notions of computation that may be partially static (independent of the input) or may take multiple inputs. If your application works fine with monads, you might as well stick with them. But if you're using a structure that's very like a monad, but isn't one, maybe it's an arrow.
The Arrow class
A computation takes inputs of some type and produces outputs of another type.
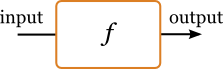
(Thanks to Cale Gibbard for the improved artwork.)
Hence Hughes defined a Haskell class of binary type constructors:
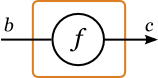
- class Arrow a where
- arr :: (b -> c) -> a b c
- -- Each function may be treated as a computation.
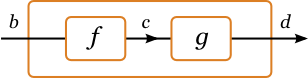
- (>>>) :: a b c -> a c d -> a b d
- -- Computations may be composed,
by connecting the output of the first to the input of the second.
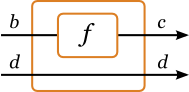
- first :: a b c -> a (b,d) (c,d)
- -- A computation may be applied to part of the input,
with the rest copied through to the output.
with a number of axioms. This and related classes are in the Control.Arrow module now distributed with all Haskell implementations. Workers in denotational semantics have independently defined equivalent structures, called Freyd-categories or (more generally) premonoidal notions of computation.
Examples
- ordinary functions
- b -> c
- Kleisli arrows
- b -> M c for any monad M
- dual Kleisli arrows
- W b -> c for any comonad W
- stream transformers
- Stream b -> Stream c. These may be used to embed dataflow languages [Pat01].
- simple automata
- Another model of dataflow languages uses the type
newtype Auto b c = Auto (b -> (c, Auto b c)) - Fudgets-style stream processors
- These are processes that can decide whether to input or output
at each step:
data SP a b = Put b (SP a b) | Get (a -> SP a b)
These may be cast as arrows [Hug00], but are usually used as dual arrows.
- state/behaviour transformers
- (S -> a) -> (S -> b) for any set S. If S represents locations, the arrow describes data parallel computations [Pat01]. If S represents time, the arrow describes behaviour transformers [CE01].
- hyperfunctions
- The weird datatype
newtype Hyper b c = H (Hyper c b -> c)can be shown to be an arrow [KLP01]. - static arrows
- F (b -> c) for "applicative" functors F. Monads are more than enough: we need only return and liftM2
In many of these cases, we can generalize from -> to any arrow (possibly constrained), yielding arrow transformers.